Giúp nhanh ạ, e cảm ơn 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: BE+CE=BC
=>BC=20+15=35 (cm)
Ta có: DE vuông góc với AB (gt)
AC vuông góc với AB (tam giác ABC vuông tại A)
=>DE//AC
Xét tam giác ABC có:
DE//AC (cmt)
=>\(\dfrac{BD}{AB}=\dfrac{BE}{BC}\)(định lý Ta-let)
=>\(\dfrac{16}{AB}=\dfrac{20}{35}\)
=>AB=28 (cm)
b. Xét tứ giác ADEK có:
góc ADE=góc DAK=góc AKE=900
=>ADEK là hình chữ nhật.
c. Ta có: AB=BD+AD
=>28=16+AD
=>AD=12(cm)
Xét tam giác ABC vuông tại A có:
AB2+AC2=BC2(định lý Ta-let)
=>282+AC2=352
=>AC=21 (cm)
Xét tam giác ABC có:
DE//AC (cmt)
=>\(\dfrac{BD}{AB}=\dfrac{DE}{AC}\)(định lý Ta-let)
=>\(\dfrac{16}{28}=\dfrac{DE}{21}\)
=>DE=12(cm)
*SADEK=AD.DE=12.12=144(cm)

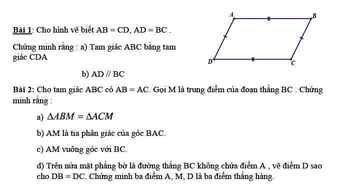
Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!



ab.ab - 4327 = 0
=> ab^2 = 4327
=>ab = \(\sqrt{4327}\)
=> ab = 65,77
Học tốt
#Kook

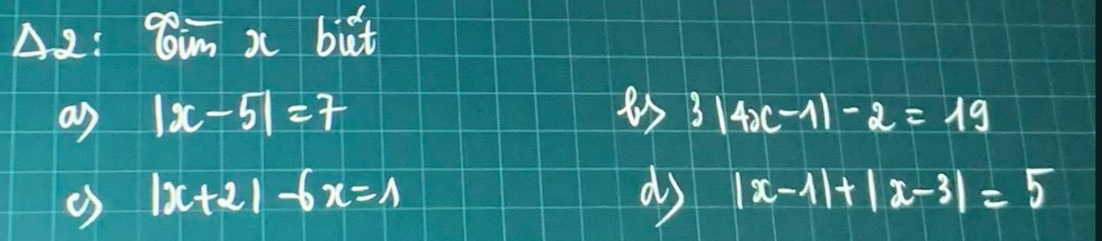 giúp em 4 câu này nhanh với ạ e cảm ơn
giúp em 4 câu này nhanh với ạ e cảm ơn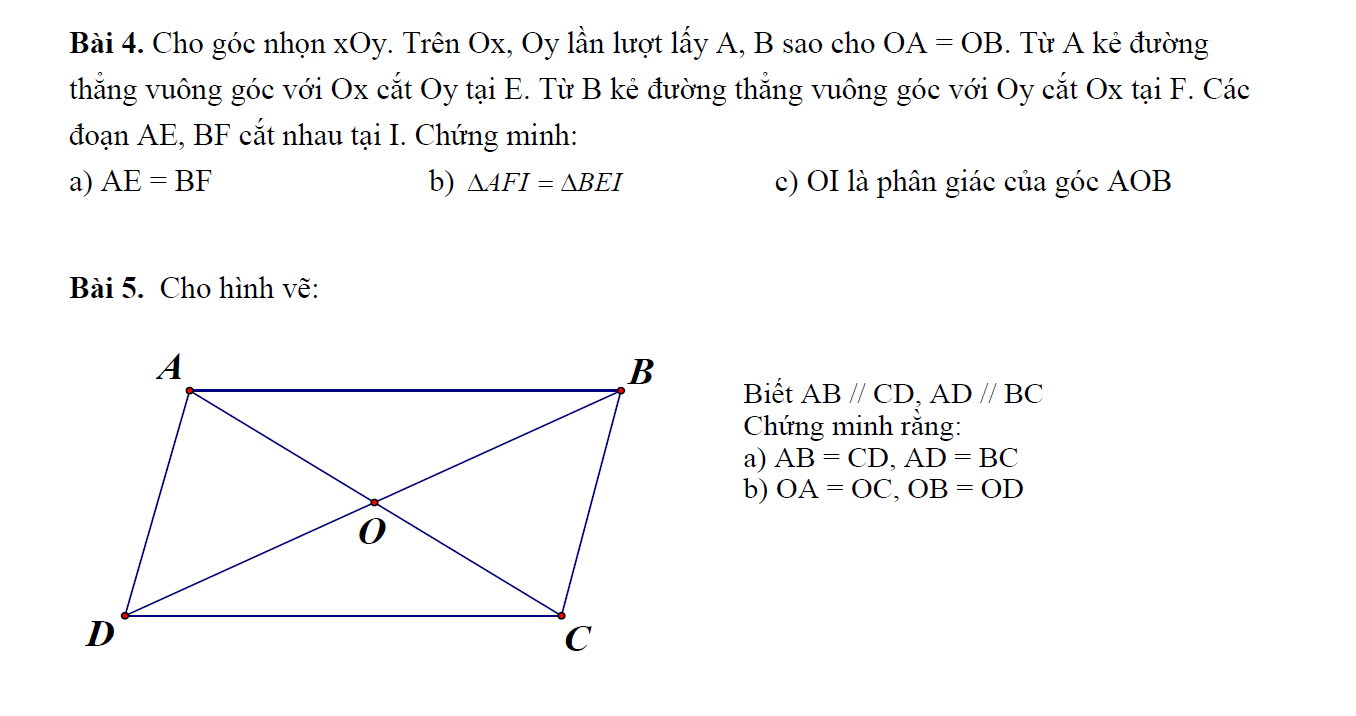 =)))
=)))

1) DC cắt AB tại H.
- Ta có: \(\widehat{DAB}+\widehat{BAC}=\widehat{DAC}\) ; \(\widehat{CAE}+\widehat{BAC}=\widehat{BAE}\).
Mà \(\widehat{DAB}=\widehat{CAE}=60^0\) (△ABD đều, △ACE đều).
=>\(\widehat{DAC}=\widehat{BAE}\)
- Xét △DAC và △BAE có:
\(\left[{}\begin{matrix}AD=AB\left(\Delta ABDđều\right)\\\widehat{DAC}=\widehat{BAE}\left(cmt\right)\\AC=AE\left(\Delta ACEđều\right)\end{matrix}\right.\)
=>△DAC = △BAE (c-g-c).
=>\(\widehat{ADC}=\widehat{ABE}\) (2 góc tương ứng).
- Ta có: \(\widehat{ADH}+\widehat{HAD}+\widehat{AHD}=180^0\) (tổng 3 góc trong △DAH).
\(\widehat{MBH}+\widehat{BMH}+\widehat{BHM}=180^0\) (tổng 3 góc trong △BMH).
Mà \(\widehat{ADH}=\widehat{MBH}\) (cmt) ; \(\widehat{BHM}=\widehat{AHD}\) (đối đỉnh).
=>\(\widehat{DAH}=\widehat{HMB}\) mà \(\widehat{DAH}=60^0\) (△ABD đều).
=>\(\widehat{HMB}=60^0\).
Mà \(\widehat{HMB}+\widehat{BMC}=180^0\) (kề bù).
=>\(60^0+\widehat{BMC}=180^0\)
=>\(\widehat{BMC}=120^0\).
2) Ta có: MF=MB (gt) nên △MBF cân tại M.
Mà \(\widehat{FMB}=60^0\) (cmt) nên △MBF đều.
=> \(\widehat{FBM}=60^0\) mà \(\widehat{ABD}=60^0\) (△ABD đều) nên \(\widehat{FBM}=\widehat{ABD}=60^0\)
Mà \(\widehat{FBH}+\widehat{ABM}=\widehat{FBM}\); \(\widehat{FBH}+\widehat{DBF}=\widehat{ABD}\).
=>\(\widehat{DBF}=\widehat{ABM}\)
- Xét △BFD và △BMA có:
\(\left[{}\begin{matrix}BD=BA\left(\Delta ABDđều\right)\\\widehat{DBF}=\widehat{ABM}\left(cmt\right)\\BF=BM\left(\Delta BMFđều\right)\end{matrix}\right.\)
=>△BFD = △BMA (c-g-c).
3) - Ta có: \(\widehat{DFB}+\widehat{BFM}=180^0\) (kề bù).
Mà \(\widehat{BFM}=60^0\) (△BFM đều) nên \(\widehat{DFB}+60^0=180^0\)
=>\(\widehat{DFB}=120^0\) mà \(\widehat{DFB}=\widehat{AMB}\) (△BFD = △BMA)
Nên \(\widehat{AMB}=120^0\)