Bộ ba số nào là ba cạnh của một tam giác vuông?
3cm ; 5 cm ; 7cm
-3 cm ; -4 cm ; -5 cm
8m ; 15 m ; 17 m
Không có bộ ba số nào thỏa mãn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2022
Tam giác cân là tam giác có `3` cạnh bằng nhau.
`=>` Loại `A, B`.
Mà trong tam giác thì tổng `2` cạnh luôn lớn hơn cạnh hcofn lại.
`=>` Loại `D ( 3 + 3 < 9)`.
`=> C`.
16 tháng 3 2022
Với mỗi bộ ba đoạn thẳng có số đo sau đây, bộ ba nào không thể là độ dài ba cạnh của một tam giác?
A. 4cm; 3cm; 4cm. B. 6cm; 8cm; 10cm.
C. 2cm; 5cm; 4cm. D. 11cm; 7cm; 18cm
CM
25 tháng 10 2019
Ta có : 4cm + 3cm = 7cm > 6cm.
⇒ Bộ ba đoạn thẳng 3cm, 4cm, 6cm thỏa mãn bất đẳng thức tam giác nên là ba cạnh của tam giác.
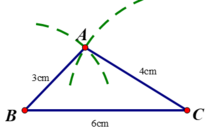
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm
- Vẽ BC = 6cm
- Dựng đường tròn tâm B bán kính 3cm ; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.
CM
29 tháng 6 2019
Ta có: 3cm + 2cm = 5cm < 6cm
⇒ Bộ ba đoạn thẳng 2cm, 3cm, 6cm không thỏa mãn bất đẳng thức tam giác nên không phải là ba cạnh của tam giác.
CM
25 tháng 10 2018
Bộ ba không thỏa mãn bất đẳng thức tam giác là 6cm, 7cm, 13cm.
Vì 6+ 7= 13 ( tổng độ dài 2 cạnh bằng độ dài còn lại – mâu thuẫn với bất đẳng thức tam giác).
Chọn (C) 6cm, 7cm, 13cm.
8m; 15m; 17m
1. \(3^2+5^2\ne7^2\) => Không phải tam giác vuông.
2. Độ dài cả 3 cạnh < 0 => Không có tam giác nào.
3. \(8^2+15^2=17^2\) => Tam giác vuông.