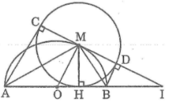
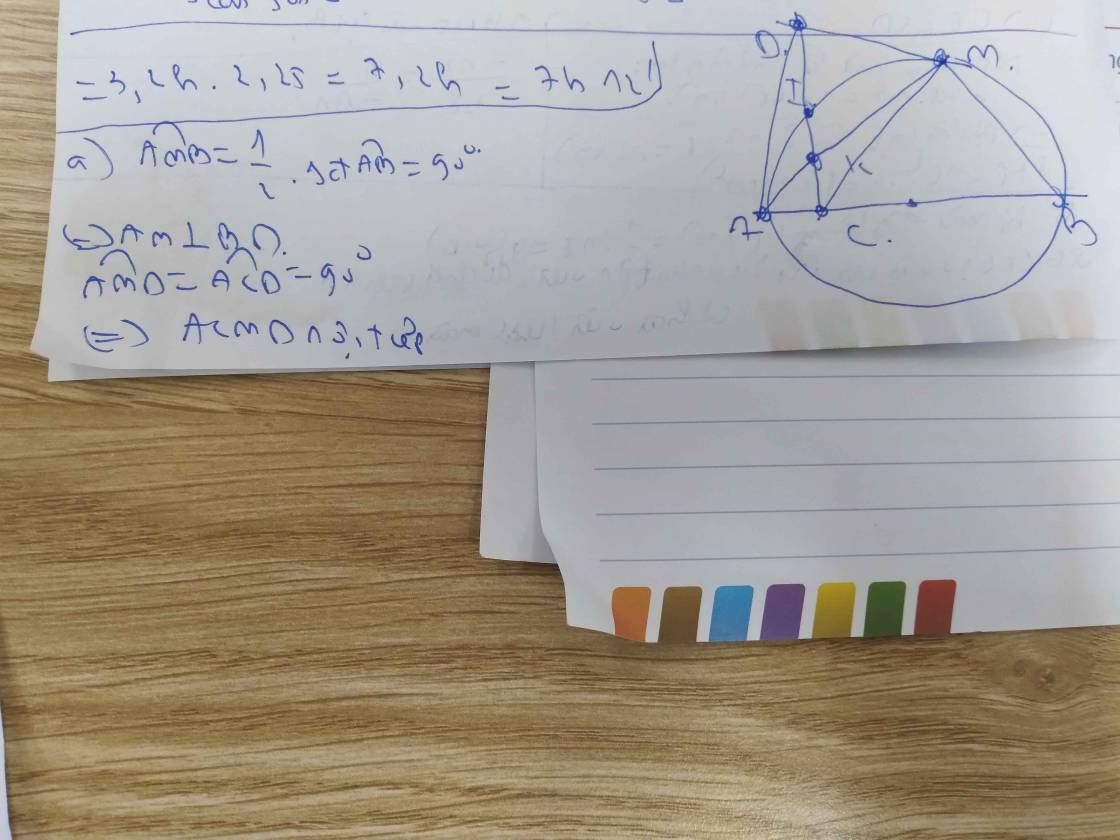
cho đường tròn tâm O đường kính AB và điểm C bất kì trên nửa đường tròn sao cho AC

NN

nguyen ngoc son

22 tháng 1 2022

cho đường tròn tâm O đường kính AB và điểm C bất kì trên nửa đường tròn sao cho AC<CB. gọi C' là điểm đối xứng của C qua AB và D là giao điểm cuả 2 tia BC, C'A. gọi K là chân đường vuông góc từ D đến Ab và D' à giao điểm của CA và DKa.cm CD.BH=HC.CD' (H là giao điểm của MC' với...

Đọc tiếp

#Toán lớp 9

0

BM

Bảo mon

14 tháng 4 2023

Cho nửa (O) đường kính AB=2R,C lad điểm bất kì nằm trên nửa đường tròn sao cho C khác A và AC

#Toán lớp 9

0

PT

Pham Trong Bach

16 tháng 1 2018

Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đén AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C và D là các tiếp điểm khác H). Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi

#Toán lớp 9

1

CM

Cao Minh Tâm

16 tháng 1 2018

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:

AC = AH và BD = BH

Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH

Suy ra: AC + BD = AH + BH = AB không đổi

Đúng(0)

LH

Lương Hoàng Bách

VIP

5 tháng 4 2023 - olm

cho nửa đường tròn tâm O đường kính AB và một điểm C nằm giữa A và B ( AC < AB). Lấy điểm M bất kì trên nửa đường tròn ( M khác A và B). Trên cùng một nửa mặt phẳng bờ AB có chứa M, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Đường thẳng qua M vuông góc với MC cắt tia Ax tại P

#Toán lớp 9

0

ND

Nghiêm Đức Trung

28 tháng 12 2021

Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên nửa đường tròn lấy điểm C bất kì (C khác A và B). Tiếp tuyến tại C và tiếp tuyến tại A cắt nhau tại M. a) Chứng minh bốn điểm, O, A, M, C cùng thuộc một đường tròn. b) AC cắt OM tại H, chứng minh AC vuông góc với OM và 2.OH OM =R mũ 2.

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

29 tháng 12 2021

a: Xét tứ giác OAMC có

\(\widehat{OAM}+\widehat{OCM}=180^0\)

Do đó: OAMC là tứ giác nội tiếp

Đúng(0)

TN

Tân Ngô Minh

17 tháng 10 2015 - olm

Cho nửa đường tròn tâm O đường kính AB. Lấy AO là đường kính vẽ nửa đường tròn tâm O' cùng phía với nửa đg tròn tâm O. một cái tuyến bất kì qua A giao nửa đường tròn tâm O' và O tại C và D. CMR C là trung điểm AD và tiếp tuyến tại C // với tiếp tuyến tại D.

b*) Nêu cách xác định điểm C sao cho BC là tiếp tuyến (O')

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 3 2023

a: góc ACO=1/2*sđ cung AO=90 độ

=>OC//BD

Xét ΔADB có

O là trung điểm của AB

OC//BD

=>C là trung điểm của AD

b: BC là tiếp tuyến của (O')

=>góc BCO'=90 độ

=>góc O'CA=góc OCB

=>góc CO'O=góc O'CO=góc O'OC

=>ΔOO'C đều

=>C thuộc (O') sao cho ΔOCO' đều

=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm

Đúng(0)

TN

Tân Ngô Minh

17 tháng 10 2015 - olm

Cho nửa đường tròn tâm O đường kính AB. Lấy AO là đường kính vẽ nửa đường tròn tâm O' cùng phía với nửa đg tròn tâm O. một cái tuyến bất kì qua A giao nửa đường tròn tâm O' và O tại C và D. CMR C là trung điểm AD và tiếp tuyến tại C // với tiếp tuyến tại D.

b*) Nêu cách xác định điểm C sao cho BC là tiếp tuyến (O')

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 3 2023

a: góc ACO=1/2*sđ cung AO=90 độ

=>OC//BD

Xét ΔADB có

O là trung điểm của AB

OC//BD

=>C là trung điểm của AD

b: BC là tiếp tuyến của (O')

=>góc BCO'=90 độ

=>góc O'CA=góc OCB

=>góc CO'O=góc O'CO=góc O'OC

=>ΔOO'C đều

=>C thuộc (O') sao cho ΔOCO' đều

=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm

Đúng(0)

TA

Thị An Nguyễn

14 tháng 3 2023

Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :a) Các tứ giác : ACMD ; BCKM nội tiếp đường trònb) CK.CD = CA.CBc) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 3 2023

loading...

Đúng(0)

DK

dan khanh

3 tháng 6 2023

cho nửa đường tròn tâm o đường kính ab trên nửa đường tròn lấy điểm c sao cho ca <cb,vẽ ch vuông góc với ab (h thuộc ab).trên cung bc lấy điểm d bất kì (d khác b và c),gọi e là giao diểm của ch và ad.

a)chứng minh tứ giác bdhe nội tiếp đường tròn

b)chứng minh ac bình phương = ae.ad

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

4 tháng 6 2023

a: góc EHB+góc EDB=180 độ

=>BDHE nội tiếp

b: Xét ΔACE và ΔADC có

góc ACE=góc ADC

góc CAE chung

=>ΔACE đồng dạng với ΔADC

=>AC^2=AE*AD

Đúng(0)

PT

Phạm Thư

29 tháng 5 2021

cho đường tròn tâm o đường kính AB trên cùng 1 nửa đường tròn (O) đường kính AB lấy 2 điểm C và D sao cho cung AC nhỏ ho7n cung AD .Gọi T là giao điểm của CD và AB .Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằ giũa cung nhỏ CD ) nối MN cắt AB tại E . cHỨNG MINH TM là tiếp tuyến của đường tròn (O) chứng minh TM^2= TC.TD . 4 điểm o, d,c,e cùng nằm trên đường...

Đọc tiếp

#Toán lớp 9

1

AT

An Thy

29 tháng 5 2021

a) Vì TO là đường kính \(\Rightarrow\angle TMO=90\) mà \(M\in\left(O\right)\Rightarrow TM\) là tiếp tuyến của (O)

b) Xét \(\Delta TMC\) và \(\Delta TDM:\) Ta có: \(\left\{{}\begin{matrix}\angle MTDchung\\\angle TMC=\angle TDM\end{matrix}\right.\)

\(\Rightarrow\Delta TMD\sim\Delta TCM\left(g-g\right)\Rightarrow\dfrac{TC}{TM}=\dfrac{TM}{TD}\Rightarrow TC.TD=TM^2\)

c) Vì đường tròn đường kính TO có tâm I và đường tròn (O) cắt nhau tại M và N \(\Rightarrow\) IO là trung trực của MN \(\Rightarrow MN\bot TO\)

mà \(\Delta TMO\) vuông tại M \(\Rightarrow TM^2=TE.TO\) (hệ thức lượng)

mà \(TC.TD=TM^2\Rightarrow TC.TD=TE.TO\Rightarrow\dfrac{TC}{TE}=\dfrac{TO}{TD}\)

Xét \(\Delta TEC\) và \(\Delta TDO:\) Ta có: \(\left\{{}\begin{matrix}\angle OTDchung\\\dfrac{TC}{TE}=\dfrac{TO}{TD}\end{matrix}\right.\)

\(\Rightarrow\Delta TEC\sim\Delta TDO\left(c-g-c\right)\Rightarrow\angle TEC=\angle TDO\Rightarrow ODCE\) nội tiếp

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP