Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC , E là điểm đối xứng với H qua I . Tứ giác AECH là hình gì :
A : Hình bình hành
B : Hình thang cân
C : Hình chữ nhật
D : Hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 12 2022
a: Xét tứ giác AHCE có
M là trung điểm chung của AC và HE
góc AHC=90 độ
DO đó: AHCE là hình chữ nhật
b: Xét tứ giác AEHB có
AE//HB
AE=HB
Do đó: AEHB là hình bình hành
c: BH=CH=12/2=6cm
\(S_{AECH}=6\cdot8=48\left(cm^2\right)\)
CM
9 tháng 6 2018
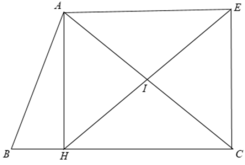
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có E A H ^ = A H C ^ = H C E ^ = C E A ^ = 90 0
⇒ AHCE là hình chữ nhật.
C
Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC , E là điểm đối xứng với H qua I . Tứ giác AECH là hình gì :
A : Hình bình hành
B : Hình thang cân
C : Hình chữ nhật
D : Hình thoi