Có 6 hành khách bước lên một đoàn tàu có 5 toa. Hỏi có bao nhiêu cách nếu: a) 6 người lên cùng 1 toa. b) 6 người lên các toa một cách tùy ý.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 5 2023
Không mất tính tổng quát, giả sử toa 1 có đúng 4 hành khách. Khi đó số cách để các hành khách lên toa 1 là \(C^4_8=70\) cách. Nếu gọi \(x,y\) lần lượt là số hành khách trên toa 2, 3 thì \(\left(x,y\right)\in\left\{\left(4;0\right);\left(3;1\right);\left(2;2\right);\left(3;1\right);\left(4;0\right)\right\}\). Khi đó có tất cả \(2\left(C^0_4+C^3_4.C^1_1\right)+C^2_4.C^2_2=16\) (cách). Vậy có tất cả là \(3.70.16=3360\) cách thỏa ycbt \(\Rightarrow\) Chọn C
CM
7 tháng 7 2019
Chọn C
Chọn toa có 3 người có 3 (toa)
Chọn 3 hành khách xếp vào toa đó có 
(cách)
Hành khách còn lại có 2 cách chọn toa
Số cách chọn là: 3. 
.2 = 24 (C).
9 tháng 5 2023
Số cách xếp là:
\(C^3_4\cdot5\cdot1\cdot4=80\left(cách\right)\)
CM
6 tháng 3 2017
Số cách lên toa của 7 người là: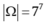 
Ta tìm số khả năng thuận lợi của A như sau
Chọn 3 toa có người lên: 
Với toa có 4 người lên ta có: 
cách chọn
Với toa có 2 người lên ta có: 
cách chọn
Người cuối cùng cho vào toa còn lại nên có 1 cách
Theo quy tắc nhân ta có: 
Do đó: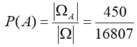 
.
Chọn A.
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 2 2023
Mỗi hành khách có 8 cách chọn toa tàu để lên, do đó không gian mẫu là: \(8^3\)
Chọn 3 toa trong 8 toa và xếp 3 hành khách vào 3 toa đó (mỗi hành khách 1 toa): \(A_8^3\) cách
Xác suất: \(\dfrac{A_8^3}{8^3}=\dfrac{21}{32}\)
a. Có 5 cách chọn 1 toa cho 6 người
b. Mỗi người có 5 cách chọn toa, do đó 6 người có \(5^6\) cách chọn
B