Với n là số tự nhiên, hãy so sánh bội chung nhỏ nhất của n^2+n+2 và 3 với n^2+n+2 ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SC
0
NL
0
KZ
3
29 tháng 7 2016
- Gọi d là ước chung lớn nhất của n và n + 2
=> n chia hết d và n + 2 chia hết d
=> ( n + 2 ) - n chia hết d
=> 2 chia hết d
=> d = 1 hoặc 2
Nếu n lẻ => d = 1
Nếu n chẵn => d = 2
Vậy ước chung lớn nhất của n và n + 2 là 1 hoặc 2
Ta có : Nếu ước chung lớn nhất của n và n + 2 = 1
thì bội chung nhỏ nhất của n và n +2 = n(n+2)
Nếu ước chung lớn nhất của n và n +2 là 2
thì bội chung nhỏ nhất của n và n +2 = n(n+2) : 2
Làm như thế này có đúng không vậy ?
DT
0
NB
0
15 tháng 12 2014
Ư(12)=(1,2,3,4,6,12)
Thay lần lượt ta có n+1=1 <=> n = 0
Bạn thay lần lượt nhé!
TN
23 tháng 12 2021
a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
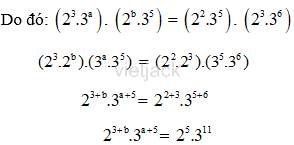
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
DN
11 tháng 11 2022
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y=
Mà xy =
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6
1 tháng 1 2022
a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
