Cho hàm số \(y=\dfrac{x^3}{3}-\left(m-1\right)x^2+3\left(m-1\right)x+1\). Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng \(\left(1;+\infty\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(g'\left(x\right)=0\Rightarrow x=0\)
Ta thấy \(g\left(x\right)\) đồng biến trên \(\left(0;+\infty\right)\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến khi \(f\left(x\right)\ge0\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) khi \(f\left(x\right)\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-4x\ge-m\) ; \(\forall x>3\)
\(\Leftrightarrow-m\le\min\limits_{x>3}\left(x^2-4x\right)\)
\(\Rightarrow-m\le-3\Rightarrow m\ge3\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2022
- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)
HP
22 tháng 3 2021
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
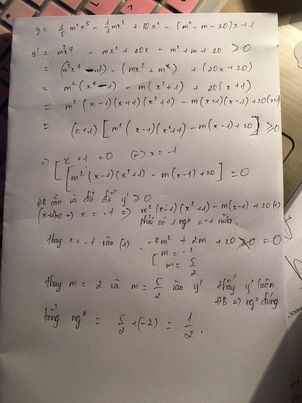
\(y'=x^2-2\left(m-1\right)x+3\left(m-1\right)\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x>1\) ta luôn có:
\(g\left(x\right)=x^2-2\left(m-1\right)x+3\left(m-1\right)\ge0\)
\(\Rightarrow\min\limits_{x>1}g\left(x\right)\ge0\)
Do \(a=1>0;-\dfrac{b}{2a}=m-1\)
TH1: \(m-1\ge1\Rightarrow m\ge2\)
\(\Rightarrow g\left(x\right)_{min}=f\left(m-1\right)=\left(m-1\right)^2-2\left(m-1\right)^2+3\left(m-1\right)\ge0\)
\(\Rightarrow\left(m-1\right)\left(4-m\right)\ge0\Rightarrow1\le m\le4\Rightarrow2\le m\le4\)
TH2: \(m-1< 1\Rightarrow m< 2\Rightarrow g\left(x\right)_{min}=g\left(1\right)=m\ge0\)
Vậy \(0\le m\le4\)