Cho tam giác ABC vuông tại A, biết AB=12cm,BC=20cm. Hãy tính diện tích tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 8 2018
Vì △ ABD và △ ABC có chung đường cao kẻ từ đỉnh A nên:
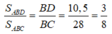
Vậy: S A B D = 3/8.S
S A D C = S A B C - S A B D = S - 3/8.S = 8/8.S - 3/8.S = 5/8.S
Vì DE // AB và AD là đường phân giác góc A nên AE = DE
Ta có: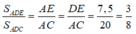 
Vậy: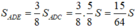 
Ta có: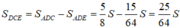 
S
8 tháng 2 2021
1) Có \(\Delta ABC\) vuông
=> S\(\Delta ABC\) = \(\dfrac{AB.AC}{2}\) = \(\dfrac{16.12}{2}\) = 96 (cm2)
2) Có \(\Delta ABC\) vuông , theo định lý Pytago ta có :
AB2 + AC2 = BC2
=> 162 + 122 = BC2
=> 400 = BC2
=> BC = 20 (cm)
Ta có : S\(\Delta ABC\) = S\(\Delta ABH\) + S\(\Delta ACH\)
=> \(\dfrac{BH.AH}{2}+\dfrac{HC.AH}{2}=S\Delta ABC\)
=> \(\dfrac{BH.AH+HC.AH}{2}=S\Delta ABC\)
=> \(\dfrac{AH.\left(BH+HC\right)}{2}=S\Delta ABC\)
=> \(\dfrac{AH.BC}{2}\) = 96
=> AH = 96 . \(\dfrac{2}{BC}\) = 96 . \(\dfrac{2}{20}\) = 9.6 (cm)
3) Có \(\Delta ABH\) vuông , theo định lý Pytago ta có :
BH2 = AB2 - AH2
=>BH2 = 162 - 9.62 = 163.84
=> BH = 12.8 (cm)
=> CH = BC - BH = 20 - 12.8 = 7.2 (cm)
NN
5
DD
4 tháng 8 2015
Tam giác ABC vuông tại A. => AB^2+AC^2=BC^2
12^2+AC^2=20^2
AC^2=400-144
AC^2=256
AC=\(\sqrt{256}=16cm\)
KN
4 tháng 8 2015
Áp dụng Pytato vào tam giác ta được :
AB^2 +AC^2 = BC^2
=> 12^2 +AC^2=20^2
=> AC^2=20^2-12^2=256
=> AC=16 (cm)
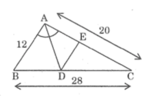
Áp dụng định lí PTG: \(AC=\sqrt{BC^2-AB^2}=16\left(cm\right)\)
Vậy \(S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot12\cdot16=96\left(cm^2\right)\)