m.n ơi giúp mk giải bài này với, mk cần gấp
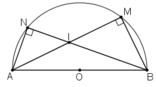
Cho đường tròn tâm O đường kính AB=2R. Gọi C và D là hai điểm thuộc đường tròn cho hai dây cung AC và BD cắt nhau tại I.
a/ Chứng minh rằng: \(\overrightarrow{AI}.\overrightarrow{AC}=\overrightarrow{AI}.\overrightarrow{AB}\) và \(\overrightarrow{BI}.\overrightarrow{BD}=\overrightarrow{BI}.\overrightarrow{BA}\)
b/ Gọi M là điểm nằm ngoài đường tròn (O). Đường thẳng qua M cắt đường tròn (O) tại hai điểm E, F. Chứng minh rằng: \(\overrightarrow{ME}.\overrightarrow{MF}=MO^2-R^2\)
mk cần gấp cho ngày mai ak mong m.n giúp mình, thank you very much
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) Vì F C H = F D H = 90 o nên tứ giác CHDF nội tiếp đường tròn tâm I đường kính FH
=> IC = ID. Mà OC = OD nên ∆ OCI = ∆ ODI (c.c.c) => COI = DOI
=> OI là phân giác của góc COD
d) Vì OC = CD = OD = R nên ∆ OCD đều => COD = 60o
Có C A D = 1 2 C O D = 30 o = > C F D = 90 o − C A D = 60 o
Xét góc nội tiếp và góc ở tâm cùng chắn cung CD của (I), có
CID = 2CFD = 120o => OIC = OID = C I D 2 = 60 o
Xét góc nội tiếp và góc ở tâm cùng chắn cung CD của (I), có
CID = 2CFD = 120o => OIC = OID = C I D 2 = 60 o
Mặt khác COI = DOI = C O D 2 = 30 o = > O I D + D O I = 90 o = > Δ O I D vuông tại D
Suy ra O I = O D sin 60 o = 2 R 3
Vậy I luôn thuộc đường tròn O ; 2 R 3

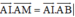 và
và 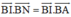
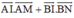 theo R.
theo R.