cho 2x+y=2010.tính giá trị nhỏ nhất của biểu thức B=1-2x+y+7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ZV
2
8 tháng 3 2017
\(B=\left|1-2x\right|+\left|y+7\right|=\left|2x-1\right|+\left|y+7\right|\)
Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) \(\forall a;b\) Ta có :
\(B=\left|2x-1\right|+\left|y+7\right|\ge\left|\left(2x-1\right)+\left(y+7\right)\right|=\left|\left(2x+y\right)+6\right|=\left|2010+6\right|=2016\)
Dấu "=" xảy ra <=> \(\left(1-2x\right)\left(y+7\right)\ge0\Leftrightarrow\hept{\begin{cases}x\le\frac{1}{2}\\y\ge-7\end{cases}}\)
Vậy \(B_{min}=2016\) tại \(x\le\frac{1}{2};y\ge7\)
TT
14 tháng 8 2020
Các bài này em áp dụng công thức \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\). Dấu "=" xảy ra khi tích \(a.b\ge0\),
a) Ta có : \(x-y=3\Rightarrow x=3+y\).
Do đó : \(B=\left|x-6\right|+\left|y+1\right|\)
\(=\left|3+y-6\right|+\left|y+1\right|=\left|3-y\right|+\left|y+1\right|\)
\(\ge\left|3-y+y+1\right|=4\)
Dấu "=" xảy ra \(\Leftrightarrow\left(3-y\right)\left(y+1\right)\ge0\)
\(\Leftrightarrow\hept{\begin{cases}-1\le y\le3\\2\le x\le6\end{cases},x-y=3}\)
Vậy giá trị nhỏ nhất của \(B=4\) \(\Leftrightarrow\hept{\begin{cases}-1\le y\le3\\2\le x\le6\end{cases},x-y=3}\)
b) Ta có : \(x-y=2\Rightarrow x=2+y\)
Do đó \(C=\left|2x+1\right|+\left|2y+1\right|\)
\(=\left|2y+5\right|+\left|2y+1\right|=\left|-2y-5\right|+\left|2y+1\right|\)
\(\ge\left|-2y-5+2y+1\right|=4\)
Các câu khác tương tự nhé em !
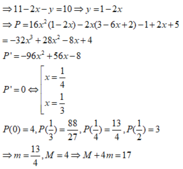
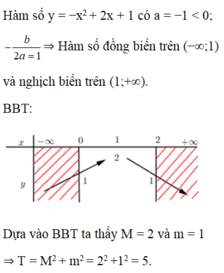
kết quả là-2002
bạn giải rõ được không?