Một lớp có 13 bạn nam và 12 bạn nữ chọn ngẫu nhiên 3 bạn. Tính xác xuất sao cho a, 3 bạn là nam b,2 bạn nam và 1 nữ có, 3 bạn nữ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không gian mẫu: \(C_5^3=10\)
Chọn 3 bạn có ít nhất 2 nữ: ta có 2 trường hợp thuận lợi là 2 nữ 1 nam và 3 bạn đều nữ
\(\Rightarrow C_2^1.C_3^2+C_3^3=7\) cách
Xác suất: \(P=\dfrac{7}{10}\)

a. \(C^1_7=7\left(cách\right)\)
b. \(C^1_3=3\left(cách\right)\)
c. Số cách không ra bạn nữ là chỉ chọn nam, vậy số cách chọn ít nhất 1 nữ là: \(7-3=4\left(cách\right)\)

Số cách chọn các bạn đi lao động là:
![]()
Gọi biến cố A: “Chọn mỗi tổ 2 bạn đi lao động, trong đó có đúng 3 bạn nữ”.
Khi đó ta có các TH sau:
+) Tổ 1 có 2 bạn nữ, tổ 2 có 1 bạn nữ và 1 bạn nam có:
![]()
+) Tổ 1 có 1 bạn nữ và 1 bạn nam, tổ 2 có 2 bạn nữ có:
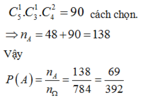
Chọn B.

Chọn B
Chọn mỗi tổ 2 bạn nên số phần tử của không gian mẫu ![]() .
.
Gọi A là biến cố : “Có đúng 3 bạn nữ trong 4 bạn đi lao động”, khi đó
TH1: Chọn 2 nữ tổ I, 1 nữ tổ II, 1 nam tổ II có ![]() .
.
TH2: Chọn 2 nữ tổ II, 1 nữ tổ I, 1 nam tổ I có ![]() .
.
Suy ra ![]() .
.
Xác suất để chọn 4 bạn đi lao động có đúng 3 bạn nữ là ![]() .
.

\(n\left(\Omega\right)=C^2_8\)
\(n\left(A\right)=C^2_5\)
=>P(A)=5/14

Chọn B.
Không gian mẫu có số phần tử là ![]() .
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: ![]() .
.
Vậy xác suất cần tính là 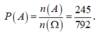 .
.
a, Gọi A là biến cố "Cả 3 bạn là nam".
\(\left|\Omega\right|=C^3_{25}\)
\(\left|\Omega_A\right|=C^3_{13}\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{C^3_{13}}{C^3_{25}}=\dfrac{143}{1150}\)
b, Gọi B là biến cố "Có 2 bạn nam và 1 bạn nữ".
\(\left|\Omega\right|=C^3_{25}\)
\(\left|\Omega_B\right|=C^2_{13}.C^1_{12}\)
\(\Rightarrow P\left(B\right)=\dfrac{\left|\Omega_B\right|}{\left|\Omega\right|}=\dfrac{C^2_{13}.C^1_{12}}{C^3_{25}}=\dfrac{234}{575}\)