1: Một lò xo nhẹ có độ cứng k=100N/m, khi treo vật nặng m lò xo giãn ra được 10cm trong giới hạn đàn hồi. Lực đàn hồi của lò xo có độ lớn là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


m =500 g=0,5 kg
Lực đàn hồi của lò xo là
\(F_{đh}=P=mg=0,5\cdot10=5\left(N\right)\)
Độ giãn của lò xo là
\(\left|\Delta l\right|=\dfrac{F_{đh}}{k}=\dfrac{5}{100}=0,05\left(m\right)=5\left(cm\right)\)

Đáp án C
Để đơn giản, ta có thể chia quá trình chuyển động của vật thành hai gia đoạn.
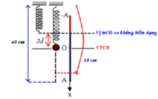
Giai đoạn chuyển động từ biên dưới đến vị trí lò xo khống biến dạng → lực đàn hồi là hợp lực của lò xo và dây tương ứng với lò xo có độ cứng k = k 1 + k 2 = 40 N / m .
Giai đoạn hai từ vị trí lò xo không biến dạng đến vị trí lò xo bị nén cực đại, lúc này dây bị chùng nên không tác dụng lực đàn hồi lên vật.
+ Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 40 = 2 , 5 cm = 0,5A.
→ Thời gian chuyển động từ biên dưới đến vị trí lò xo không biến dạng là t 1 = T 1 3 = 2 π 3 m k = 2 π 3 0 , 1 40 = π 30 s
→ Vận tốc của vật ngay thời điểm đó v 0 = 3 2 ω A = 3 2 40 0 , 1 .5 = 50 3 cm/s
+ Khi không còn lực đàn hồi của dây, ta xem vật dao động điều hòa quanh vị trí cân bằng mới, nằm dưới vị trí cân bằng cũ một đoạn = 0 , 1.10 10 − 2 , 5 = 7 , 5 c m
→ Biên độ dao động mới A ' = 2 , 5 + 7 , 5 2 + 50 3 10 2 = 5 7 ≈ 13 , 23 cm.
+ Thời gian để vật đến biên trên tương ứng là t 2 = T 2 360 0 a r cos 10 5 7 = 0 , 2 π 360 0 a r cos 10 5 7 ≈ 0 , 071 s.
→ Tổng thời gian t = t 1 + t 2 = 0 , 176 s .

Chọn B
+ Ta có: A = (lmax – lmin) : 2 = 5 (cm) và lcân bằng = (lmax + lmin) : 2 = 35 (cm).
+ Lò xo có chiều dài l = 38 cm > lcân bằng
+ Li độ của chất điểm là: x = 38 – 35 = 3cm = 0,03m.
Mà: F = k.(Δl + x)
ó 10 = 100.(Δl + 0,03)
=> Δl = 0,07m = 7cm.
=> Δlmax = 7 + 5 = 12cm.

Đáp án B
Tần số góc của dao động ω = k m = 100 0 , 2 = 10 5 rad/s → T = 0,281 s.
+ Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 2 cm
→ Kéo vật xuống vị trí lò xo giãn 6 cm rồi thả nhẹ → lò xo sẽ dao động với biên độ A = 6 – 2 = 4 cm.
+ Với E d = E d h ↔ E – E t = E d h → 1 2 k A 2 − 1 2 k x 2 = 1 2 k Δ l 0 + x 2 → 2 x 2 + 2 Δ l 0 x + Δ l 0 2 − A 2 = 0
Thay các giá trị đã biết vào phương trình, ta thu được x 2 + 2 x – 6 = 0 → hoặc x = 1,65 cm hoặc x = –3,65 cm.
→ Thời gian gần nhất kể từ thời điểm ban đầu (vật đang ở biên là) Δ t min = a r cos 1 , 65 4 360 0 0 , 281 = 51 , 3 m s

ü Đáp án D
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 4 cm
+ Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng lên → lực đàn hồi bằng lực phục hồi
- k x = - k Δ l 0 - x ⇒ x = 0 , 5 Δ l 0 = 2 c m




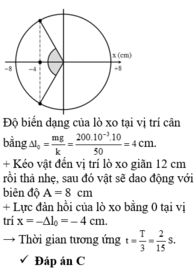
Độ lớn lực đàn hồi là:
\(F_{đh}=k.\Delta l=100.10.10^{-2}=10N\)
dạ câu trả lời
Độ lớn lực đàn hồi là:
Fđh=k.Δl=100.10.10−2=10N