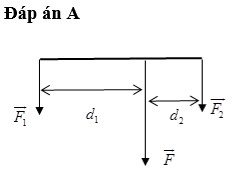
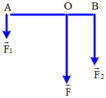
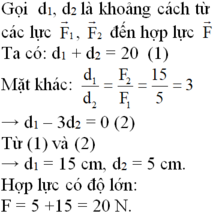xác định hợp lực f của hai lực song song cùng chiều vecto f1 f2 đặt 2 đầu của một thanh nhẹ AB= 20cm. Biết F1=5N F2= 15N.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
4 tháng 7 2018
Đáp án A
Vì hai lực song song và cùng chiều nên:
F = F 1 + F 2 ⇒ F 2 = F − F 1 = 15 − 5 = 10 ( N )
Áp dụng công thức:
F 1 . d 1 = F 2 . d 2 ⇒ 5 ( 0 , 3 − d 2 ) = 10 d 2 ⇒ d 2 = 0 , 1 ( m ) = 10 ( c m )
VT
14 tháng 10 2017
Vì hai lực song song và cùng chiều nên:
F = F 1 + F 2 ⇒ F 2 = F − F 1 = 25 − 15 = 10 ( N )
Áp dụng công thức
F 1 . d 1 = F 2 . d 2 ⇒ 15 ( 0 , 2 − d 2 ) = 10 d 2 ⇒ d 2 = 0 , 12 ( m ) = 12 ( c m )
VT
3 tháng 6 2018
Gọi O là giao điểm của giá hợp lực F → với AB.
a. Hai lực F → 1 , F → 2 cùng chiều:
Điểm đặt O trong khoảng AB.
Ta có: { O A O B = F 2 F 1 = 3 O A + O B = A B = 4 c m
=> OA = 3cm; OB = 1cm
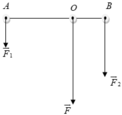
Vậy F → có giá qua O cách A 3cm, cách B 1cm, cùng chiều với F → 1 , F → 2 và có độ lớn F = 8N
b. Khi hai lực ngược chiều:
Điểm đặt O ngoài khoảng AB, gần B (vì F2 > F1):
{ O A O B = F 2 F 1 = 3 O A − O B = A B = 4 c m
=> OA = 6cm; OB = 2cm.
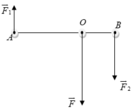
Vậy có giá đi qua O cách A 6cm, cách B 2cm, cùng chiều với F → 2 và có độ lớn F 4N.
