CHỨNG MINH RẰNG : VỚI MỌI PHÂN SỐ BÉ HƠN 1 CÓ CẢ TỬ SỐ VÀ MẪU SỐ ĐỀU LÀ SỐ NGUYÊN DƯƠNG, KHI TA CỘNG CẢ TỬ SỐ VÀ MẪU SỐ VỚI CÙNG 1 SỐ NGUYÊN n THÌ TA ĐƯỢC 1 PHÂN SỐ LỚN HƠN PHÂN SỐ BAN ĐẦU
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
22 tháng 12 2021
\(\frac{a}{b}=\frac{a+2}{bx2}\Rightarrow2xaxb=axb+2xb\Rightarrow axb=2xb\)
\(\Rightarrow a=2\Rightarrow b=1\)
\(\frac{a}{b}=\frac{2}{1}\)
12 tháng 3 2021
Bài 1 : bằng phân số ban đầu
Bài 2 : nhỏ hơn phân số ban đầu
Bài 3 : lớn hơn phân số ban đầu
CM
4 tháng 1 2020
Gợi ý: Khi ta nhân 1 phân số với số tự nhiên, ta chỉ việc nhân tử số của phân số với số tự nhiên đó và giữ nguyên mẫu số. Vậy nhân tử số của phân số với 2 , giữ nguyên mẫu số tức là ta gấp phân số đó lên 2 lần. Bài toán được chuyển về dạng: tìm 2 số biết hiệu và tỉ số.
Giải
Nếu nhân tử số của phân số với 2 và giữ nguyên mẫu số thì ta được phân số mới gấp 2 lần phân số ban đầu. Ta có sơ đồ sau:
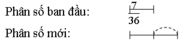
Phân số ban đầu là: 7/36: (2 - 1) = 7/36
Thử lại: 7 x 2 36 - 7 36 = 7 36
16 tháng 8 2017
Giả sử phan số lớn hơn 1 la\(\frac{a}{b}\)(a,b\(\in\)N , a>b>0 ) và c số dương cộng vào tử và mẫu
Ta có : \(\frac{a+c}{b+c}\)= \(\frac{\left(a+c\right)\times b}{\left(b+c\right)\times b}\) = \(\frac{ab+cb}{\left(b+c\right)\times b}\)
\(\frac{a}{b}\)= \(\frac{a\times\left(b+c\right)}{b\times\left(b+c\right)}\)= \(\frac{ab+ac}{\left(b+c\right)\times b}\)
Ta có: Vì a>b nên : ac > cb
=> ab+cb<ab+ac => \(\frac{ab+cb}{\left(b+c\right)\times b}\) < \(\frac{ab+ac}{\left(b+c\right)\times b}\)
Do đó: \(\frac{a+c}{b+c}\)< \(\frac{a}{b}\)
Vậy bài toán đã được chứng minh
(Mi thì cũng ngơ ngơ như con vịt ,bài dễ mà ko biết làm)
MN
10 tháng 4 2021
\(\text{Phân số là : }\) \(\dfrac{x+12}{x}\)
\(\text{Lấy cả tử và mẫu trừ cho 3 đơn vị thì được 1 phân số bằng với}\) \(\dfrac{1}{4}:\)
\(\dfrac{x+12-3}{x-3}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{x+9}{x-3}=\dfrac{1}{4}\)
\(\Leftrightarrow\left(x+9\right)\cdot4=x-3\)
\(\Leftrightarrow x=-13\)
\(\text{Phân số ban đầu là : }\) \(\dfrac{1}{13}\)
18 tháng 5 2015
Đặt lại yêu cầu đề bài :
So sánh hai phân số \(\frac{a}{b}\) và \(\frac{a}{c}\) với a, b, c \(\in\) N* và b < c.
Ta có \(\frac{a}{b}=\frac{ac}{bc}\) ; \(\frac{a}{c}=\frac{ab}{bc}\)
Do b < c và a > 0 nên ab < ac.
Vậy \(\frac{ac}{bc}>\frac{ab}{bc}\) tức là \(\frac{a}{b}>\frac{a}{c}\).
suy ra điều phải chứng minh.
