Trong mặt phẳng tọa độ oxy, cho các điểm G(1;-2) và A thuộc Oy thỏa mãn G là trọng tâm của tam giác . Tọa độ véctơ 2AB là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tọa độ trọng tâm G của tam gác MNP là:
x G = x M + x N + x P 3 = 0 + ( − 3 ) + 9 3 = 2 y G = y M + y N + y P 3 = 4 + 2 + ( − 3 ) 3 = 1 ⇒ G ( 2 ; 1 )
Đáp án D

Chọn D.
M(1;0), N(2;2), P(-1;3) là điểm biểu diễn các số phức trên .
Hai tam giác EFH và MNP có 3 trung tuyến trùng nhau từng đôi một nên có cùng trọng tâm G.
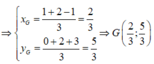

Thay x=0 vào y=x+2013, ta được:
y=0+2013=2013
Thay y=0 vào y=x+2013, ta được:
x+2013=0
hay x=-2013

\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)




Đề thiếu. Bạn coi lại đề.