Cho hàm số y = 2x + 2 (d) và (d’) y = (2 – m)x (với m khác 2). Tìm các giá trị của m để đường thẳng (d’) cắt đường thẳng (d) tại điểm có hoành độ âm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
6 tháng 1 2019
Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
KT
6 tháng 1 2019
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)
20 tháng 3 2023
Thay x=-1 vào (P), ta được:
y=-2*(-1)^2=-2
Thay x=-1và y=-2 vào (d), ta được:
-(m+1)-m-3=-2
=>-m-1-m-3=-2
=>-2m-4=-2
=>2m+4=2
=>m=-1
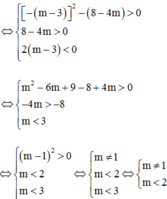
PT hoành độ giao điểm:
\(2x+2=\left(2-m\right)x\\ \Leftrightarrow2x+\left(m-2\right)x+2=0\\ \Leftrightarrow mx=-2\Leftrightarrow m=-\dfrac{2}{x}\\ \text{Mà }x< 0\Leftrightarrow m>0\)
Vậy \(m>0;m\ne2\) thỏa mãn yêu cầu đề