Bài 1: Từ điểm A bên ngoài đường tròn (O), vẽ hai tiếp tuyến AB,AC với đường tròn (O),(B,C là 2 tiếp điểm).Vẽ đường kính BD, gọi H là giao điểm của AO và BC.
a) chứng minh \(AO\perp BC\) tại H và CD // OA
b) vẽ OK vuông góc CD tại K.chứng minh OK là phân giác của góc COD
c) tia OK cắt AC tại M. chứng minh MD là tiếp tuyến của (O).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC(3)
b: Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD(4)
Từ (3) và (4) suy ra CD//OA

1: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
2: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC
góc EBC=1/2*sđ cung EC=90 độ
=>EB vuông góc BC
=>EB//OA
góc BCD=1/2*sđ cung BD=90 độ
=>CD vuông góc BC
=>CD//OA
=>góc AiF=góc CDF
=>góc AIF=góc ACF
=>AFIC nội tiếp
=>góc AIC=góc AFC=90 độ
góc AFC+góc EFC=90+90=180 độ
=>E,F,A thẳng hàng

a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC và H là trung điểm của BC
b: Xét (O) co
ΔBDC nội tiếp
BD là đường kính
=>ΔBCD vuông tại C
=>DC//OA
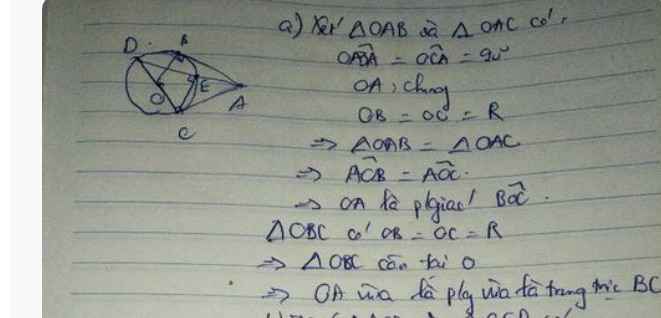

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC