Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó; ΔABD=ΔACD
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD

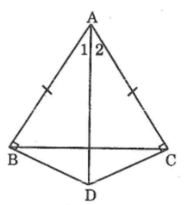
Xét hai tam giác vuông ABD và ACD, ta có:
∠(ABD) =∠(ACD) =90o
Cạnh huyền AD chung
AB = AC (giả thiết)
⇒ ΔABD= ΔACD (cạnh huyền, cạnh góc vuông)
Suy ra: ∠(A1 ) =∠(A2) (hai góc tương ứng)
Suy ra AD là tia phân giác góc A

Xét tam giác ADB và tam giac ADC có :
AD chung
Góc ABD=góc ACD=90 0
AB=AC(2 tam giác cân tại a)
=>tam giác ADB=tam giác ADC (ch-cgv)
=>góc BAD = góc CAD (góc tương ứng)
Vậy AD là tia phân giác góc A
Duyệt nha
Xét tam giác ADB và tam giác ADC có:
AD chung
góc ABD=góc ACD=90 độ
AB=AC(tam giác ABC cân tại A)
=> tam giác ADB=tam giác ADC(ch-cgv)
=> góc BAD=góc CAD(góc tương ứng)
Vậy AD là tia phân giác góc A
tik cho mk nha các bn

a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC
Ta có: O nằm trên đường trung trực của AB(gt)
mà OG⊥AB(gt)
nên G là trung điểm của AB
Ta có: O nằm trên đường trung trực của AC(gt)
mà OF⊥AC(gt)
nên F là trung điểm của AC
Ta có: \(AG=\dfrac{AB}{2}\)(G là trung điểm của AB)
\(AF=\dfrac{AC}{2}\)(F là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AG=AF
Xét ΔAGO vuông tại G và ΔAFO vuông tại F có
AO chung
AG=AF(cmt)
Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{GAO}=\widehat{FAO}\)(hai góc tương ứng)
hay \(\widehat{BAO}=\widehat{CAO}\)
mà tia AO nằm giữa hai tia AB,AC
nên AO là tia phân giác của \(\widehat{BAC}\)(đpcm)
c) Xét ΔAOB và ΔAOC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAO}=\widehat{CAO}\)(cmt)
AO chung
Do đó: ΔAOB=ΔAOC(c-g-c)
Suy ra: OB=OC(hai cạnh tương ứng)
Ta có: \(\widehat{ABC}+\widehat{KBC}=\widehat{ABK}\)(tia BC nằm giữa hai tia BA,BK)
nên \(\widehat{ABC}+\widehat{KBC}=90^0\)(1)
Ta có: \(\widehat{ACB}+\widehat{KCB}=\widehat{ACK}\)(tia CB nằm giữa hai tia CA,CK)
nên \(\widehat{ACB}+\widehat{KCB}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}+\widehat{KBC}=\widehat{ACB}+\widehat{KCB}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{KBC}=\widehat{KCB}\)
Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)(cmt)
nên ΔKBC cân tại K(Định lí đảo của tam giác cân)
Suy ra: KB=KC(hai cạnh bên)
Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)
Suy ra: \(\widehat{BCE}=\widehat{CBD}\)(hai góc tương ứng)
hay \(\widehat{HBC}=\widehat{HCB}\)
Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)(cmt)
nên ΔHBC cân tại H(Định lí đảo của tam giác cân)
Suy ra: HB=HC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: HB=HC(cmt)
nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Ta có: KB=KC(cmt)
nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)
Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)

a,Ta có: tam giác ABC cân tại A => AB=AC và góc ABC=góc ACB
Mà \(BD⊥AB,CD⊥AC\Rightarrow\widehat{B_1}=\widehat{C_1}=90^0\)
\(\Rightarrow180^0-90^0-\widehat{ABC}=180^0-90^0-\widehat{ACB}\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\)
=> \(\Delta DBC\) là tam giác cân tại D.
=> DB=DC
b, \(\widehat{ABC}=\widehat{ACB},\widehat{DBC}=\widehat{DCB}\Rightarrow\widehat{ABC}+\widehat{DBC}=\widehat{ACB}+\widehat{DCB}\Rightarrow\widehat{ABD}=\widehat{ACD}\)
Xét \(\Delta ABD\) và \(\Delta ACD\)
\(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{ABD}=\widehat{ACD}\left(cmt\right)\\DB=DC\left(cmt\right)\end{cases}}..............\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\)
\(\Rightarrow\widehat{BAO}=\widehat{CAO}\)
Xét \(\Delta BAO\) và \(\Delta CAO\)
\(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{BAO}=\widehat{CAO}\left(cmt\right)\\AO:chung\end{cases}..........\Rightarrow\Delta BAO=\Delta CAO\left(c.g.c\right)}\)
\(\Rightarrow\hept{\begin{cases}OB=OC\\\widehat{BOA}=\widehat{COA}.Mà:\widehat{BOA}+\widehat{COA}=180^0\end{cases}\Rightarrow\hept{\begin{cases}O.là.trung.điểm.BC\\\widehat{BOA}=\widehat{COA}=\frac{180^0}{2}=90^0\end{cases}}}\)
=> AD là đường trung trực của BC

a) Ta có: \(\widehat{ABC}+\widehat{MBC}=\widehat{ABM}\)(tia BC nằm giữa hai tia BA,BM)
nên \(\widehat{ABC}+\widehat{MBC}=90^0\)(1)
Ta có: \(\widehat{ACB}+\widehat{MCB}=\widehat{ACM}\)(tia CB nằm giữa hai tia CA,CM)
nên \(\widehat{ACB}+\widehat{MCB}=90^0\)(2)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)(3)
Từ (1), (2) và (3) suy ra \(\widehat{MBC}=\widehat{MCB}\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)
nên ΔMBC cân tại M(Định lí đảo của tam giác cân)
b) Xét ΔABM vuông tại B và ΔACM vuông tại C có
AB=AC(ΔABC cân tại A)
BM=CM(ΔMBC cân tại M)
Do đó: ΔABM=ΔACM(hai cạnh góc vuông)
⇒\(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
mà tia AM nằm giữa hai tia AB,AC
nên AM là tia phân giác của \(\widehat{BAC}\)(đpcm)
Ta có: ΔABM=ΔACM(cmt)
nên \(\widehat{BMA}=\widehat{CMA}\)(hai góc tương ứng)
mà tia MA nằm giữa hai tia MB,MC
nên MA là tia phân giác của \(\widehat{BMC}\)(đpcm)
c) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: MB=MC(ΔMBC cân tại M)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Từ (4) và (5) suy ra AM là đường trung trực của BC
hay AM⊥BC(đpcm)

a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC
Ta có: O nằm trên đường trung trực của AB(gt)
mà OG⊥AB(gt)
nên G là trung điểm của AB
Ta có: O nằm trên đường trung trực của AC(gt)
mà OF⊥AC(gt)
nên F là trung điểm của AC
Ta có: AG=AB2AG=AB2(G là trung điểm của AB)
AF=AC2AF=AC2(F là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AG=AF
Xét ΔAGO vuông tại G và ΔAFO vuông tại F có
AO chung
AG=AF(cmt)
Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)
Suy ra: ˆGAO=ˆFAOGAO^=FAO^(hai góc tương ứng)
hay ˆBAO=ˆCAOBAO^=CAO^
mà tia AO nằm giữa hai tia AB,AC
nên AO là tia phân giác của ˆBACBAC^(đpcm)
c) Xét ΔAOB và ΔAOC có
AB=AC(ΔABC cân tại A)
ˆBAO=ˆCAOBAO^=CAO^(cmt)
AO chung
Do đó: ΔAOB=ΔAOC(c-g-c)
Suy ra: OB=OC(hai cạnh tương ứng)
Ta có: ˆABC+ˆKBC=ˆABKABC^+KBC^=ABK^(tia BC nằm giữa hai tia BA,BK)
nên ˆABC+ˆKBC=900ABC^+KBC^=900(1)
Ta có: ˆACB+ˆKCB=ˆACKACB^+KCB^=ACK^(tia CB nằm giữa hai tia CA,CK)
nên ˆACB+ˆKCB=900ACB^+KCB^=900(2)
Từ (1) và (2) suy ra ˆABC+ˆKBC=ˆACB+ˆKCBABC^+KBC^=ACB^+KCB^
mà ˆABC=ˆACBABC^=ACB^(hai góc ở đáy của ΔABC cân tại A)
nên ˆKBC=ˆKCBKBC^=KCB^
Xét ΔKBC có ˆKBC=ˆKCBKBC^=KCB^(cmt)
nên ΔKBC cân tại K(Định lí đảo của tam giác cân)
Suy ra: KB=KC(hai cạnh bên)
Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
ˆEBC=ˆDCBEBC^=DCB^(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)
Suy ra: ˆBCE=ˆCBDBCE^=CBD^(hai góc tương ứng)
hay ˆHBC=ˆHCBHBC^=HCB^
Xét ΔHBC có ˆHBC=ˆHCBHBC^=HCB^(cmt)
nên ΔHBC cân tại H(Định lí đảo của tam giác cân)
Suy ra: HB=HC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: HB=HC(cmt)
nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Ta có: KB=KC(cmt)
nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)
Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)
a) Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABD=ΔACD(cạnh huyền-cạnh góc vuông)
b) Ta có: ΔABD=ΔACD(cmt)
nên \(\widehat{BAD}=\widehat{CAD}\)(hai góc tương ứng)
mà tia AD nằm giữa hai tia AB,AC
nên AD là tia phân giác của \(\widehat{BAC}\)