cho hàm số y=x^2 có đồ thị (P). Gọi A và B là 2 điểm thuộc (P) lần lượt có hoành độ là -1 và 2. Viết phương trình đường thẳng AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
6 tháng 5 2021
Lời giải:
a) $y_M=\frac{-x_M^2}{2}=\frac{-(-3)^2}{2}=\frac{-9}{2}$
Đường thẳng $OM$ có dạng: $y=ax$
$\Rightarrow y_M=ax_M\Leftrightarrow \frac{-9}{2}=a.(-3)$
$\Rightarrow a=\frac{3}{2}$
Vậy ĐT $OM$ là: $y=\frac{3}{2}x$
b) Gọi PTĐT $CE$ có dạng $y=ax+b$
PT hoành độ giao điểm giữa $(P)$ và $CE$ là:
$\frac{-x^2}{2}-ax-b=0$
$\Leftrightarrow x^2+2ax+2b=0(*)$
$(P)$ và $CE$ cắt nhau tại 2 điểm có hoành độ $-1;2$ nghĩa là PT $(*)$ nhân $x=-1$ và $x=2$ là nghiệm
\(\Rightarrow \left\{\begin{matrix} 1-2a+2b=0\\ 4+4a+2b=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{-1}{2}\\ b=-1\end{matrix}\right.\)
Vậy PTĐT $CE$ có dạng $y=-\frac{1}{2}x-1$
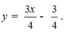
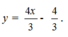
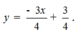
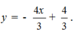
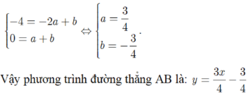
- Thay x = -1 và x = 2 vào hàm số ( P ) ta được :
\(\left[{}\begin{matrix}y=1\\y=4\end{matrix}\right.\)
=> Đường thẳng AB đi qua 2 điểm ( -1; 1 ) ; ( 2 ; 4 )
- Gọi đường thẳng AB có dạng y = ax + b
- Thay hai điểm trên lần lượt vào phương trình đường thẳng ta được :
\(\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
Vậy phương trình đường thẳng AB có dạng : y = x + 2 .