Câu 1: Một tam giác có chiều cao bằng \(\dfrac{3}{4}\) cạnh đáy. Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích tăm thêm 12 dm\(^2\). Tính chiều cao và cạnh đáy của tam giácCâu 2: Một khu vườn hình chữ nhật có chu vi bằng 48m. Nếu tăng chiều rộng lên bốn lần và chiều dài lên ba lần thì chu ci khu vươn sẽ là 162 m. Hãy tính diện tích của khu vườn ban...
Đọc tiếp
Câu 1: Một tam giác có chiều cao bằng \(\dfrac{3}{4}\) cạnh đáy. Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích tăm thêm 12 dm\(^2\). Tính chiều cao và cạnh đáy của tam giác
Câu 2: Một khu vườn hình chữ nhật có chu vi bằng 48m. Nếu tăng chiều rộng lên bốn lần và chiều dài lên ba lần thì chu ci khu vươn sẽ là 162 m. Hãy tính diện tích của khu vườn ban đầu
cạnh đáy. Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích của nó tăng thêm 12 
. Tính chiều cao và cạnh đáy của tam giác.
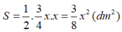
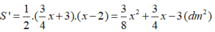
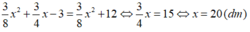
Câu 2:
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của khu vườn(Điều kiện: \(\left\{{}\begin{matrix}a>0\\b>0\\a\ge b\end{matrix}\right.\))
Vì chu vi của khu vườn là 48m nên ta có phương trình:
2(a+b)=48
hay a+b=24(1)
Vì khi tăng chiều rộng lên 4 lần và chiều dài lên 3 lần thì chu vi của khu vườn là 162m nên ta có phương trình:
\(2\cdot\left(3a+4b\right)=162\)
\(\Leftrightarrow3a+4b=81\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=24\\3a+4b=81\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=72\\3a+4b=81\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-b=-9\\a+b=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=9\left(nhận\right)\\a=24-9=15\left(nhận\right)\end{matrix}\right.\)
Diện tích ban đầu của khu vườn là:
\(S=ab=9\cdot15=135\left(m^2\right)\)