Gọi S(n) là tổng tất cả các chữ số của số nguyên dương n khi biểu diễn nó trong hệ thập phân. Biết rằng với mọi số nguyên dương n thì ta có 0<S(n)<=n. Tìm số nguyên dương n sao cho S(n)=n^2- 2011n+ 2010
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
27 tháng 12 2021
Tớ không hiểu.
Số may mắn là số gì?
6 = 3 + 2 + 1 hay sao?
29 tháng 6 2023
program tim_nguon_nho_nhat;
const
MAX_NUMBER = 10000;
var
M, nguon_nho_nhat: Integer;
function TinhTongChuSo(num: Integer): Integer;
var
sumOfDigits: Integer;
begin
sumOfDigits := 0;
while num > 0 do
begin
sumOfDigits := sumOfDigits + (num mod 10);
num := num div 10;
end;
TinhTongChuSo := sumOfDigits;
end;
function TimNguonNhoNhat(M: Integer): Integer;
var
N, M_temp, M_digits, nguon_nho_nhat: Integer;
begin
M_temp := M;
nguon_nho_nhat := MAX_NUMBER;
for N := 1 to M_temp do
begin
M_digits := TinhTongChuSo(N) + N;
if M_digits = M_temp then
begin
if N < nguon_nho_nhat then
nguon_nho_nhat := N;
end;
end;
if nguon_nho_nhat = MAX_NUMBER then
TimNguonNhoNhat := 0
else
TimNguonNhoNhat := nguon_nho_nhat;
end;
begin
Readln(M);
nguon_nho_nhat := TimNguonNhoNhat(M);
if nguon_nho_nhat = 0 then
Writeln('0')
else
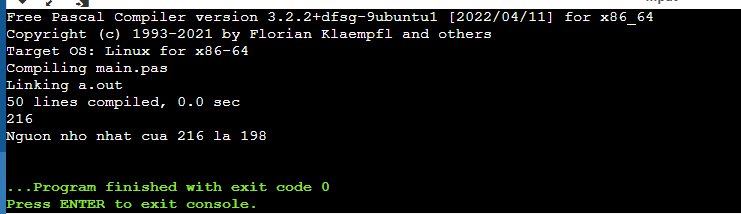
Writeln('Nguon nho nhat cua ', M, ' la ', nguon_nho_nhat);
end.
\(^∗\)Xét \(n=2011\)thì \(S\left(2011\right)=2011^2-2011.2011+2010=2010\)(vô lí)
\(^∗\)Xét \(n>2011\)thì \(n-2011>0\)do đó \(S\left(n\right)=n\left(n-2011\right)+2010>n\left(n-2011\right)>n\)(vô lí do \(S\left(n\right)\le n\))
* Xét \(1\le n\le2010\)thì \(\left(n-1\right)\left(n-2010\right)\le0\Leftrightarrow n^2-2011n+2010\le0\)hay \(S\left(n\right)\le0\)(vô lí do \(S\left(n\right)>0\))
Vậy không tồn tại số nguyên dương n thỏa mãn đề bài