Cho đường tròn $O$ đường kính $AB$ và dây cung $AC$. Chứng tỏ rằng $\text{sđ } \widehat{BAC}=\frac{1}{2} \text{sđ } \overgroup{BC}$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

DT
17 tháng 1 2021
Ta có OA = OC = bán kính đường tròn (O)
=> Tam giác OAC cân tại O => \(\widehat{A_1}=\widehat{C_1}\)
Do \(\widehat{O_1}\) là góc ngoài tại O của tam giác OAC
=> \(\widehat{O_1}\) = \(\widehat{A_1}+\widehat{C_1}\) = 2.\(\widehat{A_1}\) hay \(\widehat{A_1}\) = \(\dfrac{1}{2}\).\(\widehat{O_1}\) (đpcm)
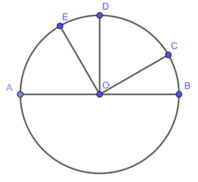
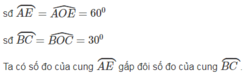
Xét tam giascOAC cân tại O nên ta có góc \(\widehat{CAO}=\widehat{ACO}\)
mà ta có \(sd \widebat{BC}=\widehat{BOC}=\widehat{OCA}+\widehat{CAO}=2\widehat{CAO}=2\widehat{CAB}\)
vajay ta cos dpcm