Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án A
Gọi u 1 , d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: u 5 = - 15 u 20 = 60 .
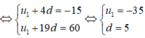
Vậy S 10 = 10 2 . ( 2 u 1 + 9 d ) = - 125

Gọi u1, d lần lượt là số hạng đầu và công sai của cấp số cộng.
Ta có: 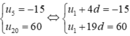
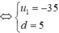
Vậy ![]()
![]()
Chọn đáp án A.
*Chú ý tổng n số hạng đầu của cấp số cộng bằng ![]()

Chọn đáp án A
Gọi u1, d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: u 5 = - 15 u 20 = 60
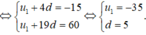
Vậy S 10 = 10 2 . ( 2 u 1 + 9 d ) = - 125

Đáp án C.
Gọi số hạng đầu và công sai của CSC (un) là u1, d ta có
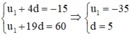
Suy ra ![]()

Đáp án D
Ta có u 5 + 3 u 3 − u 2 = − 21 3 u 7 − 2 u 4 = − 34 ⇔ u 1 + 4 d + 3 u 1 + 2 d − u 1 − d = − 21 3 u 1 + 6 d − 2 u 1 + 3 d = − 34
⇔ 3 u 1 + 9 d = − 21 u 1 + 12 d = − 34 ⇔ u 1 = 2 d = − 3 ⇒ S 15 = u 1 + u 15 2 .15 = u 1 + u 1 + 14 d 2 .15 = − 285



Hmm, cái công thức Sn mỗi lần viết dài kinh :(
\(u_5=u_1+4d=15;u_9=u_1+8d=-1\) \(\Rightarrow\left\{{}\begin{matrix}d=...\\u_1=...\end{matrix}\right.\)
\(\Rightarrow u_{100}=u_1+99d=...\)
\(u_1=u_1\)
\(u_2=u_1+d\)
\(u_3=u_1+2d\)
.....
\(u_n=u_1+\left(n-1\right)d\)
\(\Rightarrow S_n=u_1+u_2+...+u_n=u_1+u_1+d+...+u_1.\left(n-1\right)d=n.u_1+d+2d+...+\left(n-1\right)d\)
\(=n.u_1+\left(1+2+...+\left(n-1\right)\right)d=n.u_1+\dfrac{d\left(n-1\right).n}{2}=\dfrac{n\left[2u_1+\left(n-1\right)d\right]}{2}\)
Thay số vô và ... bấm máy, chắc zậy :))