Cho hàm số y = f(x) = ax4 + bx3 + cx2 + dx + e (a≠0) có đồ thị (C) cắt trục hoành tại bốn điểm phân biệt là A(x1; 0), B(x2 ; 0), C(x3 ; 0), D(x4;0), với x1, x2, x3, x4 theo thứ tự lập thành cấp số cộng và hai tiếp tuyến của (C) tại A, B vuông góc với nhau. Tính giá trị của biếu thức S = (f ' (x3) + f ' (x4))2020
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Giả thiết
![]()
Đặt
![]()
thì
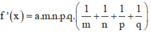
Và
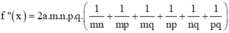
Khi đó, phương trình
![]() (vô nghiệm)
(vô nghiệm)
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.

Ta có
![]()
Đồ thị hàm số ![]() cắt trục hoành tại bốn điểm phân biệt bên phương trình
cắt trục hoành tại bốn điểm phân biệt bên phương trình ![]() , với
, với ![]() là các nghiệm.
là các nghiệm.
Suy ra
![]()
![]()
![]()
![]()
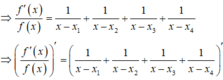
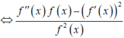
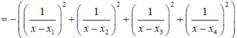
Nếu ![]() với
với ![]() thì
thì ![]() ,
, ![]()
![]() .
.
Nếu ![]() thì
thì 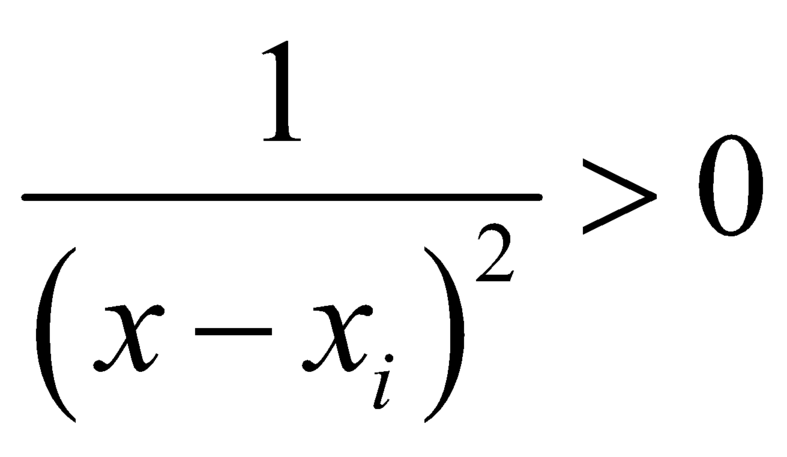 ,
, ![]() .
.
Suy ra ![]()
![]() .
.
Vậy phương trình ![]() vô nghiệm hay phương trình
vô nghiệm hay phương trình ![]() vô nghiệm.
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A

Chọn đáp án B
Ta có f ' x = 4 a x 3 + 3 b x 2 + 2 c x + d
và f ' ' x = 2 6 a x 2 + 3 b x + c
Suy ra g x = f ' x 2 - f ' ' x . f x
Đồ thị hàm số y = f x = a x 4 + b x 3 + c x 2 + d x + e cắt trục hoành tại 4 điểm phân biệt có hoành độ x 1 , x 2 , x 3 , x 4 phương trình f x = 0 có 4 nghiệm x 1 , x 2 , x 3 , x 4
Suy ra f x = a x - x 1 x - x 2 x - x 3 x - x 4
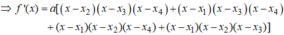
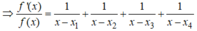
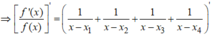
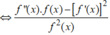
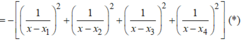
*Khi x = x i i = 1 , 2 , 3 , 4 thì
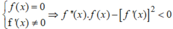
nên g x > 0
*Khi x ≠ x i ∀ i = 1 , 2 , 3 . 4 thì
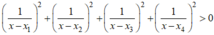
và f 2 x > 0
Từ (*) suy ra
![]()

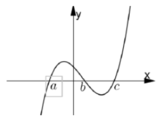
Ta có bảng biến thiên như hình vẽ bên.
Vì f( b) < 0 nên rõ ràng có nhiều nhất 2 giao điểm.

Chọn B.

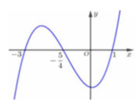
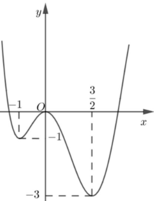
Phương trình f ( x ) + m = 0 ⇔ f ( x ) = - m có bốn nghiệm thực phân biệt khi và chỉ khi đường thẳng y=-m cắt đồ thị hàm số đã cho tại bốn điểm phân biệt ⇔ 1 - < m < 0 ⇔ 0 < m < 1
Chọn đáp án C.

Chọn đáp án C
Phương trình f x + m = 0
⇔ f x = - m có bốn nghiệm thực phân biệt
khi và chỉ khi đường thẳng y = - m cắt đồ thị hàm số đã cho tại bốn điểm phân biệt
![]()










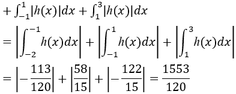

Do \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e\) có 4 nghiệm pb \(x_1;x_2;x_3;x_4\)
\(\Rightarrow f\left(x\right)=a\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\)
Ta có:
\(f'\left(x\right)=a\left[\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)+\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_2\right)\left(x-x_4\right)\right]\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a\left(x_1-x_2\right)\left(x_1-x_3\right)\left(x_1-x_4\right)\\f'\left(x_2\right)=a\left(x_2-x_1\right)\left(x_2-x_3\right)\left(x_2-x_4\right)\\f'\left(x_3\right)=a\left(x_3-x_1\right)\left(x_3-x_2\right)\left(x_3-x_4\right)\\f'\left(x_4\right)=a\left(x_4-x_1\right)\left(x_4-x_2\right)\left(x_4-x_3\right)\end{matrix}\right.\)
Mà tiếp tuyến tại A và B vuông góc \(\Leftrightarrow f'\left(x_1\right).f'\left(x_2\right)=-1\) (1)
Do \(x_1;x_2;x_3;x_4\) lập thành 1 CSC, giả sử công sai của CSC là \(d\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=x_1+d\\x_3=x_1+2d\\x_4=x_1+3d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a.\left(-d\right).\left(-2d\right).\left(-3d\right)=-6ad^3\\f'\left(x_2\right)=a.d.\left(-d\right).\left(-2d\right)=2ad^3\\f'\left(x_3\right)=a.2d.d.\left(-d\right)=-2ad^3\\f'\left(x_4\right)=a.3d.2d.d=6ad^3\end{matrix}\right.\)
Thế vào (1): \(-12a^2d^6=-1\Leftrightarrow12a^2d^6=1\)
\(\Rightarrow f'\left(x_3\right)+f'\left(x_4\right)=4ad^3\)
\(\Rightarrow S=\left(4ad^3\right)^{2020}=\left(16a^2d^6\right)^{1010}=\left(\dfrac{4}{3}.12a^2d^6\right)^{1010}=\left(\dfrac{4}{3}\right)^{1010}\)
Bài gì mà dễ sợ :(