Cho tam giác ABC.Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AB, AE =AC a, Chứng minh tam giác ABC = tam giác ADE b, Gọi AM là tia phân giác góc BCA , AN là phân giác góc DAE c, Kẻ AH vuông góc BC, AI vuông góc DE. Chứng minh H,A,I thẳng hàng ( nếu được bạn có thể vẽ hình giúp mình)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

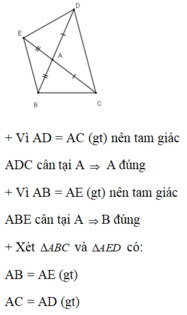
( Hình tự vẽ nha )
Ta có : AB = AE ( gt )
AD = AC ( gt )
Do đó : AB + AD = AC + AE
=> BD = EC
=> Tứ giác BDEC là hình thang ( vì trong hình thang có hai đường chéo bàng nhau )

xét tam giác EAD và tam giác ABC có:
-AD=AB
- góc EAD= góc BAC
-AE=EC
Ta suy ra tam giác EAD = tam giác ABC (c-g-c)
=> góc EDA= góc ABC
mà 2 góc này pử vị trí so le trong
=> ED//AB
=>BCDE LÀ HÌNH THANG

hai tam giác EAD = BAC ( c - g -c)
=> góc DEA = CBA
tam giác EAB đông dạng CAD (c - g - c)
=> goc AEB = ACD
=> EB // CD
lại có BED = BEA + AED
góc EBC = EBA + ABC
mà góc BEA = EBA ( tam giác BAE cân taịA)
AED = ABC (cmt)
=> BCDE la hinh thang can