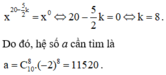Hệ số của trong khai triển của nhị thức Niu tơn ( 3 - x ) 9 là
A. - C 9 7
B. C 9 7
C. 9 C 9 7
D. - 9 C 9 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Số hạng trong khai triển có dạng là :
\(T_{k+1}=C_{10}^k.x^{10-k}.\left(-2\right)^k\)
b, Số hạng chứa \(x^8\) \(\Leftrightarrow x^{10-k}=x^8\)
\(\Leftrightarrow10-k=8\)
\(\Leftrightarrow k=10-8\)
\(\Leftrightarrow k=2\)
Hệ số của số hạng chứa \(x^8\)là :
\(T_3=C_{10}^2.\left(-2\right)^2=180\)

Ta có: 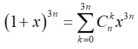
Chọn x=1. Ta có tổng hệ số bằng: ![]()
Lại có: 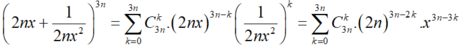
Số hạng không chứa x suy ra ![]()
Do đó số hạng không chứa x là: ![]()
Chọn D.

Đáp án A
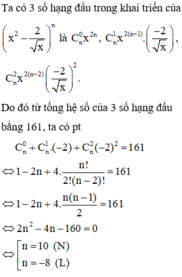
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
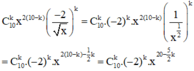
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho