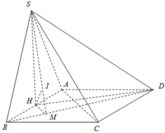
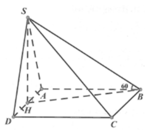
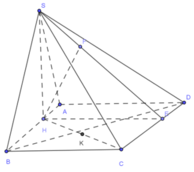
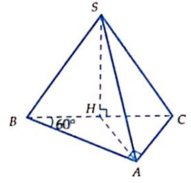
Cho hình chóp S . A B C D có đáy là hình vuông cạnh a , S D = a 17 2 . Hình chiếu vuông góc H của S lên mặt A B C D là trung điểm của đoạn A B . Gọi K là trung điểm của . Tính khoảng cách giữa hai đường S D và H K theo a
A. a 3 7
B. a 3 5
C. a 21 5
D. 3 a 5



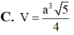
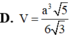
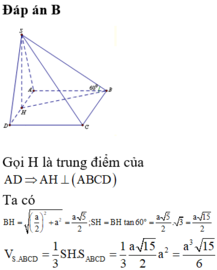
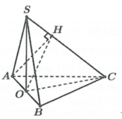


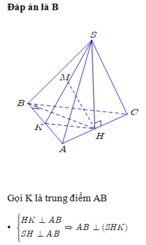
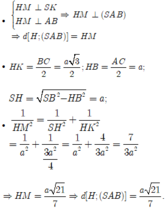
Đáp án là B.
Ta có H K / / B D ⇒ H K / / S B D ⇒ d H K ; S D = d H K ; S B D = d H ; S B D .
Dựng H M ⊥ B D , H I ⊥ S M
Do H M ⊥ B D và S H ⊥ B D nên B D ⊥ S H M ⇒ H I ⊥ S B D
H M = 1 2 A O = a 2 4 , H D = A H 2 + A D 2 = a 5 2 , S H = S D 2 − H D 2 = a 3
H I = S H . H M S H 2 + H M 2 = a 3 . a 2 4 a 3 2 + a 2 4 2 = a 3 5