Một hộp đựng tấm thẻ được đánh số từ 1 đến 9. Một bạn rút ngẫu nhiên đồng thời 3 tấm thẻ. Tính xác suất để tổng 3 số ghi trên thẻ được rút chia hết cho 3
A. 5 14
B. 9 14
C. 3 14
D. 1 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 1 2017
Chọn B.
Số cách rút hai thẻ chẵn là C 10 2 . Số cách rút ra hai thẻ trong đó có một thẻ ghi số chia hết cho 4 còn thẻ kia ghi số lẻ là .
Vậy xác suất cần tìm là C 5 1 C 5 2
CM
10 tháng 3 2019
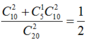
Đáp án C
Rút ngẫu nhiên 3 thẻ trong 15 thẻ có C 15 3 cách => n ( Ω ) = C 15 3 = 455 .
Gọi X là biến cố “ tổng ba số ghi trên ba thẻ rút được". Khi đó 1 ≤ x , y ≤ 15 x + y + z ⋮ 3
Từ số 1 đến số 15 gồm 5 số chia hết cho 3 (N1), 5 số chia hết cho 3 dư 1 (N2) và 5 số chia hết cho 3 dư 2 (N3).
TH1: 2 số x, y, z thuộc cùng 1 loại N1, N2 hoặc N3 => có C 5 3 + C 5 3 + C 5 3 = 30 cách.
TH2: 3 số x, y, z mỗi số thuộc 1 loại => có C 5 1 + C 5 1 + C 5 1 = 125 cách.
=> Số kết quả thuận lợi cho biến cố X là n(X) = 30 + 125 = 155.
Vậy P = n ( X ) n ( Ω ) = 31 91 .
.
.
.
.
CM
23 tháng 9 2019
Đáp án D
Số phần tử của không gian mẫu là 
.
Bộ 3 số có tổng chia hết cho 3 sẽ có bộ số dư là 
và 
.
Trong các số từ 1 đến 60 có 20 số chia hết cho 3, 20 số chia 3 dư 1 và 20 số chia 3 dư 2.
Vậy số cách chọ ra bộ 3 tấm thẻ có tổng các số trên thẻ chia hết cho 3 là
cách
Vậy xác suất cần tính là 
.
CM
25 tháng 11 2018
Đáp án D
Vậy số cách chọ ra bộ 3 tấm thẻ có tổng các số trên thẻ chia hết cho 3 là
5 tháng 5 2023
Số phần tử của không gian mẫu \(\left|\Omega\right|=C^2_{20}\)
Gọi A là biến cố: "Tổng hai số trên hai tấm thẻ được rút ra bằng 10."
Gọi \(\left(m,n\right)\) là nghiệm của \(m+n=10\). Phương trình này có tất cả \(C^{2-1}_{10-1}-1=8\) (\(-1\) ở đây là bỏ đi nghiệm \(\left(m;n\right)=\left(5;5\right)\)). Do đó \(\left|A\right|=8\) \(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{\left|\Omega\right|}=\dfrac{8}{C^2_{20}}=\dfrac{4}{95}\)
Đáp án là A