Tính các góc của một tam giác vuông, biết tỉ số 2 cạnh góc vuông là 3:4. Chu vi tam giác đó là 36 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2022
Gọi hai cạnh góc vuông là a, b; cạnh huyền là c;
Dựa vào tính chất Pi-ta-go, tỉ số của cạnh huyền là: \(\sqrt{3^2}+4^2=\sqrt{9}+16=5\);
Dựa vào tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3;\)
Vì a/3 = 3 => a = 3*3 = 9;
b/4 = 3 => b = 4*3 = 12;
c/5 = 3 => c = 5*3 = 15;
CM
28 tháng 2 2019
Gọi độ dài hai cạnh góc vuông của tam giác lần lượt là a và b. Gọi c là độ dài cạnh huyền (a, b, c > 0)
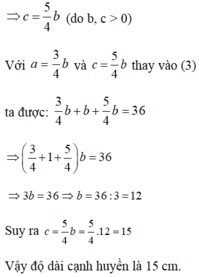
Đáp án B
NP
0
TU
Tìm các cạnh của một tam giác vuông biết tỉ số các cạnh góc vuông là 3 : 4, chu vi tam giác bằng 36.
3
D
15 tháng 3 2016
gọi các cạnh góc vuông lần lượt là a,b;
ta có:\(\frac{a}{3}=\frac{b}{4}=k\Rightarrow a=3k;b=4k\)
áp dụng định lí py-ta-go, ta có: cạnh huyền =\(\sqrt{\left(9k^2+16k^2\right)}\)
ta có:3k+4k+\(\sqrt{\left(9k^2+16k^2\right)}\)=36
7k+\(\sqrt{25k^2}\)=36
\(7k+\sqrt{\left(5k\right)^2}=36\)
\(7k+5k=36\)
\(12k=36\Rightarrow k=36:12=3\)
cạnh góc vuông lớn nhất của tam giác đó là: 3x4=12(cm)
cạnh góc vuông nhỏ nhất của tam giác đó là: 3x3=9(cm)
cạnh huyền của tam giác đó là: \(\sqrt{\left(12^2+9^2\right)}=\sqrt{225}=15\left(cm\right)\)
