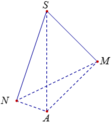
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S A = a và S A ⊥ A B C D . Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho S N = 2 S D . Tính thể tích V của khối tứ diện ACMN
A. V = a 3 8
B. V = a 3 36
C. V = a 3 6
D. V = a 3 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phương pháp tọa độ (cách này tính toán khá phức tạp nên chỉ nêu ra để học sinh thấy không phải bài toán nào cũng dùng phương pháp tọa độ cũng nhanh nhất)
Ta chọn hệ trục tọa độ như hình vẽ và chọn a = 1.
Ta có:
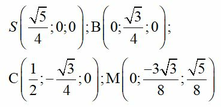
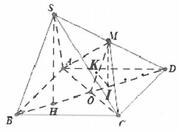

Chọn D
Thể tích khối chóp S. ABCD là:
![]()
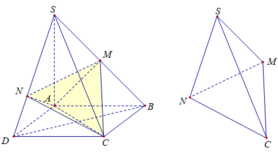
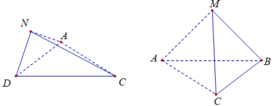
Thể tích tứ diện SMNC là:
![]() .
.
Thể tích tứ diện NACD là:
![]() .
.
Thể tích tứ diện MABC là:
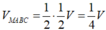 .
.
Thể tích tứ diện SAMN là:
![]() .
.
Mặt khác ta có:
![]()
Suy ra:
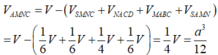
Đáp án D
Gọi O = A C ∩ B D ⇒ V S . A B C D = a 3 3 ,
Vì O M / / S D ⇒ N D / / O M ⇒ N D / / M A C
Vì d N , A M C = d D , A M C = d B , A M C ⇒ V N . A M C = V D . M A C = V B . M A C = 1 4 V S . A B C D = a 3 12