CHO TAM GIAC ABC CÂN TẠI A. TRÊN TIA ĐỐI CỦA BC LẤY ĐIỂM D, TRÊN TIA ĐỐI CÚA CB LẤY ĐIỂM E SAO CHO BD=CE. CHỨNG MINH TAM GIÁC ADE LÀ TAM GIÁC CÂN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
31 tháng 5 2017
Hình vẽ:
Giải:
Vì tam giác \(ABC\) cân tại \(A\):
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\) ( góc bù )
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB=AC \) \(\left(gt\right)\)
\(\widehat{ABD}=\widehat{ACE}\) \(\left(cmt\right)\)
\(BD=CE \) \(\left(gt\right)\)
Do đó: \(\Delta ABD=\Delta ACE\) \(\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) ( cặp cạnh tương ứng )
\(\Rightarrow\Delta ADE\) cân tại \(A\).
20 tháng 1 2018
Bài làm
Bạn tự vẽ hình nhé
Vì tam giác ABCABC cân tại A:
⇒ˆABC=ˆACB⇒ABC^=ACB^
⇒ˆABD=ˆACE⇒ABD^=ACE^ ( góc bù )
Xét ΔABDΔABD và ΔACEΔACE có:
AB=ACAB=AC (gt)
ˆABD=ˆACEABD^=ACE^ (cmt)
BD=CEBD=CE (gt)(gt)
Do đó: ΔABD=ΔACEΔABD=ΔACE (c.g.c)(c.g.c)
⇒AD=AE⇒AD=AE ( cặp cạnh tương ứng )
⇒ΔADE⇒ΔADE cân tại A
CM
1 tháng 6 2018
Chứng minh được tam giác ABD = tam giác ACE (c-g-c) => AD = AE
Từ đó tam giác ADE cân tại A.
4 tháng 12 2022
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
4 tháng 12 2022
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
CM
4 tháng 4 2018
theo đầu bài ta có góc abc=góc acb
mà góc ABD+ABC =180(kề bù)
góc ACE+ACB =180 (kề bù)
suy ra góc ABD =ACE
xét tam giác ABD và tam giác ACE
AB=AC(gt)
góc ABD=ACE
BD=CE(gt)
Do đó tam giác ABD=tam giác ACE (c.g.c)
nên AD=AE (2 cạnh tương ứng)
suy ra tam giác ADE cân
5 tháng 4 2020
Ta có: tam giác ABC cân tại A
=> AB = AC
Góc ABC = góc ACB
=> góc ABD = góc ACE
Xét tam giác ADB và tam giác AEC, ta có:
AB = AC (gt) (1)
góc ABD = góc ACE (cmt) (2)
BD = CE (gt) (3)
Từ (1), (2) và (3), suy ra:
tam giác ADB = tam giác AEC (c.g.c)
=> AD = AE (2 cạnh tương ứng)
=> tam giác ADE cân tại A
CM
7 tháng 11 2017
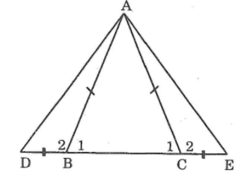
*) Ta có: ΔABC cân tại A
BD = CE (giả thiết)
Suy ra: ΔABD = ΔACE (c.g.c)
⇒ AD = AE ( hai cạnh tương ứng)
*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)
17 tháng 4 2016
Bạn tự vẽ hình nha!
a.
Ta có:
- B1 + B2 = 180
- C1 + C2 = 180
mà B1 = C1 (tam giác ABC cân tại A)
=> B2 = C2 (1)
Xét tam giác ADB và tam giác AEC:
AB = AC (tam giác ABC cân tại A)
B2 = C2 (theo 1)
BD = CE (gt)
=> Tam giác ADB = ACE (c.g.c)
=> AD = AE (2 cạnh tương ứng)
=> Tam giác ADE
b.
Xét tam giác AHB vuông tại A và tam giác AKC vuông tại K:
AB = AC (tam giác ABC cân tại A)
A1 = A2 (tam giác ADB = tam giác AEC)
=> Tam giác AHB = Tam giác AKC (cạnh huyền - góc nhọn)
=> BH = CK (2 cạnh tương ứng)
AH = AK (2 cạnh tương ứng)
c.
Xét tam giác HDB vuông tại H và tam giác KEC vuông tại K:
BH = CK (theo câu b)
BD = CE (gt)
=> Tam giác HDB = Tam giác KEC (cạnh huyền - cạnh góc vuông)
Ta có:
DBH = IBC (2 góc đối đỉnh)
KCE = ICB (2 góc đối đỉnh)
mà DBH = KCE (tam giác HDB = tam giác KEC)
=> IBC = ICB
=> Tam giác IBC cân tại I
tam giác ABC cân =>góc B=góc C
=>góc ABD=góc ACE (dựa vào 2 góc kề bù)
Xét tam giác ABD và tam giác ACE có
AB=AC(tam giác ABC cân)
góc ABD= góc ACE(cmt)
BD=CE(GT)
=>tam giác ABD = tam giác ACE (c-g-c)
=>AD=AE(2 cạnh tương ứng)
=>tam giác ADE cân tại A