Cho hình lăng trụ ABC.A'B'C'có thể tích bằng a 3 . Gọi M, N, P lần lượt là tâm của các mặt bên và G là trọng tâm tam giác ABC . Tính thể tích V của khối tứ diện GMNP
A. V = a 3 24
B. V = a 3 8
C. V = a 3 12
D. V = a 3 16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
2 tháng 4 2016
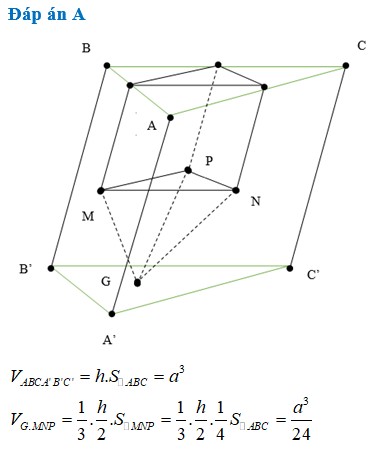
_ Thể tích khối lăng trụ :
Gọi D là trung điểm của BC ta có : \(BC\perp AD\Rightarrow BC\perp A'D\Rightarrow\widehat{ADA'}=60^0\)
Ta cso \(AA'=AD.\tan\widehat{ADA'}=\frac{3a}{2};S_{ABC}=\frac{a^2\sqrt{3}}{4}\)
Do đó \(V_{ABC.A'B'C'=}S_{ABC}.AA'=\frac{3a^2\sqrt{3}}{8}\)
- Bán kính mặt cầu ngoại tiếp tứ diện GABC :
Ta có I là giao điểm của GH với đường trung trực của AG trong mặt phẳng (AGH)
Gọi E là trung điểm của AG, ta có :
\(R=GI=\frac{GE.GA}{GH}=\frac{GA^2}{2GH}\)
Ta có :
\(GH=\frac{AA'}{3}=\frac{a}{2};AH=\frac{a\sqrt{3}}{3};GA^2=GH^2+AH^2=\frac{7a^2}{12}\)
Do đó \(R=\frac{7a^2}{2.12}.\frac{2}{a}=\frac{7a}{12}\)
CM
11 tháng 7 2019
Đáp án C.
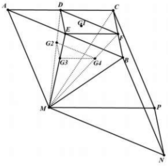
Phương pháp
So sánh diện tích đáy và chiều cao của các khối chóp.
Cách giải
Gọi D, E, F lần lượt là trung điểm của AC, AB, BC.
Vì G 2 ; G 3 ; G 4 là trọng tâm các tam giác MAC, MAB, MBC nên
G 2 ∈ M D ; M G 2 = 2 D G 2 G 3 ∈ M E ; M G 3 = 2 E G 3 G 4 ∈ M F ; M G 4 = 2 F G 4 ⇒ G 2 G 3 G 4 / / D E F ⇒ V 1 = V E . G 2 G 3 G 4 = F G 3 M G 3 . V M . G 2 G 3 G 4 = 1 2 V M . G 2 G 3 G 4
Lại có
V M . G 2 G 3 G 4 V M D E F = M G 2 . M G 3 . M G 4 M D . M E . M F = 2 3 . 2 3 . 2 3 = 8 27
⇒ V 1 = 1 2 8 27 V M D E F = 4 27 V M D E F
Lại có
S D E F = 1 4 S A B C ⇒ V M . D E F = 1 4 V M . A B C = 1 4 . 1 3 V = 1 12 V
Vậy
V 1 = 4 27 . V 12 = V 81
CM
12 tháng 3 2017
Gọi M là trung điểm BC: BC = 2a; AG = 2 3 AI = 2 a 3 ; A ' A G ^ = 60 o .
Suy ra: A ' G = A G tan 60 o = 2 a 3 3
Ta có: V = S A B C . A ' G = 1 2 AB.AC.A'G
= 1 2 a. a 3 . 2 a 3 3 = a 3
Vậy V 3 + V a 3 - 1 = a
Đáp án B
CM
11 tháng 6 2017
Chọn D
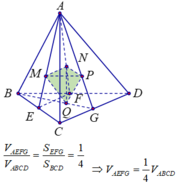
(Do E, F, G lần lượt là trung điểm của BC, BD, CD).
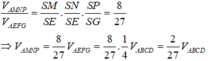
Do mặt phẳng (MNP) (BCD) nên
