Tìm tất cả các giá trị thực của m để hàm số f x = x 1 − 1 x khi x

PT

Pham Trong Bach

23 tháng 10 2017

Tìm tất cả các giá trị thực của m để hàm số f x = x + 1 − 1 x khi x > 0 x 2 + 1 − m khi x ≤ 0 liên tục trên ℝ . A. m = 3 2 . B. m = 1 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

23 tháng 10 2017

Đáp án B

Đúng(0)

PT

Pham Trong Bach

29 tháng 3 2017

Tìm tất cả các giá trị thực của m để hàm số f ( x ) = x + 1 - 1 x k h i x > 0 x 2 + 1 - m k h i x ≤ 0 liên tục trên R A. m = 3 2 B. m = 1 2 C. m = - 2 D. m = - 1 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

29 tháng 3 2017

Đúng(0)

PT

Pham Trong Bach

30 tháng 8 2019

Tìm tất cả các giá trị của m để hàm số f ( x ) = 1 - x - 1 + x x k h i x < 0 m + 1 - x 1 + x k h i x ≥ 0 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

30 tháng 8 2019

Đáp án B

Đúng(0)

PT

Pham Trong Bach

10 tháng 4 2019

Cho hàm số f(x) = x - m 2 + m x + 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng – 2.

A. m= 1

B. m= -2

C. m= -1

D. m= -1 hoặc m= 2

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 4 2019

Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]

Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m²+m

Theo bài ta có:

-m²+ m= -2 nên m= -1 hoặc m= 2.

Chọn D.

Đúng(0)

PT

Pham Trong Bach

20 tháng 2 2017

Tìm tất cả các giá trị thực của m để hàm số f x = x + 1 − 1 x k h i x > 0 x 2 + 1 − m k h i x ≤ 0 liên tục trên R. A. m = 3 2 . B. m = 1 2 . C. m = -2 D. m = ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

20 tháng 2 2017

Đáp án là B

Đúng(0)

S

Scarlett

20 tháng 6 2023

Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số \(m\) để \(f\left(x\right)0,\forall x\in\left(0;1\right)\)., ( )Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >, (...

Đọc tiếp

#Toán lớp 10

1

GH

Gia Huy

20 tháng 6 2023

Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)

\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)

\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)

Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)

\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)

Đúng(2)

S

Scarlett

20 tháng 6 2023

Có cách nào khác nx ạ?

Đúng(0)

PT

Pham Trong Bach

23 tháng 10 2018

Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ , với f (x) > 0 và f (0) = 1. Biết rằng f ' ( x ) + 3 x x - 2 f ( x ) = 0 , ∀ x ∈ ℝ . Tìm tất cả các giá trị thực của tham số m để phương trình f x + m = 0 có bốn nghiệm thực phân biệt. A. 1 < m < e 4 B. - e 6 < ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

23 tháng 10 2018

Đáp án C

Bảng biến thiên của hàm số f(x) là

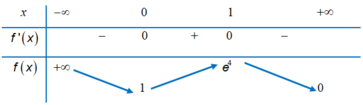
Hàm số f x là hàm số chẵn trên ℝ nên đồ thị của hàm số nhận trục tung làm trục đối xứng. Do đó phương trình f ( x ) + m = 0 có bốn nghiệm thực phân biệt khi và chỉ khi phương trình f ( x ) + m = 0 có hai nghiệm dương phân biệt hay phương trình f ( x ) = - m có hai nghiệm dương phân biệt

⇔ 1 < - m < e 4 ⇔ - e 4 < m < - 1

Đúng(0)

PT

Pham Trong Bach

6 tháng 7 2018

Cho hàm số y = f(x) có f'(x)>0 ∀ x ∈ ℝ . Tìm tập hợp tất cả các giá trị thực của x để f 1 x < f ( 1 ) ...

Đọc tiếp