Cho hàm số y = a x 3 + b x 2 + c x + d ; với a, b, c, d là các số thực, có đồ thị như hình vẽ bên:
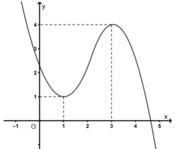
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 x 2 = m có đúng 3 nghiệm thực phân biệt ?
A. 1
B. 2
C. 3
D. Vô số.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)

a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)

\(y=\dfrac{1}{2}\left(x^2-1\right)\) không phải hàm số bậc nhất
Chọn A