Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60 ° . Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
A. V = a 3 3 2
B. V = 3 a 3 3 4
C. V = a 3 3 8
D. V = 3 a 3 3 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
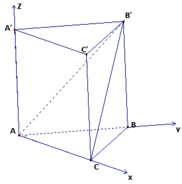
Vì tam giác ABC vuông cân tại A, cạnh BC = a√6 nên AB = AC = a√3.
Chọn hệ trục tọa độ Oxyz sao cho A (0;0;0), B (0; a√3; 0), C (a√3;0;0), A' (0;0;z) (z > 0).
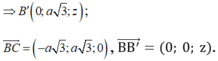
VTPT của (BCC'B') là:
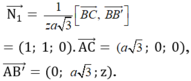
VTPT của mặt phẳng (BA'C) là:
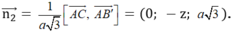
Vì góc giữa mặt phẳng và mặt phẳng bằng nên:
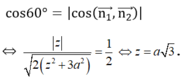
Vậy thể tích của khối lăng trụ ABC.A'B'C' là:
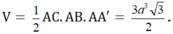

Đáp án B
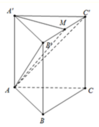
Ta có: S A B C = 1 2 A B . A C . sin A = a 2 3 4
Gọi M là trung điểm của B ' C ' khi đó
B ' C ' ⊥ A ' M B ' C ' ⊥ A A ' ⇒ B ' C ' ⊥ A ' M A
Suy ra A ' M A ⏜ = A B ' C ' ' A ' B ' C ' ⏜ = 30 °
Lại có A ' M = A ' B sin 30 ° = a 2 ⇒ A A ' = A ' M t a n 30 ° = a 2 3
⇒ V A B C . A ' B ' C ' = S A B C . A A ' = a 3 8

Đáp án A
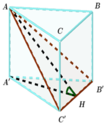
Góc giữa A B ' C ' và mặt đáy là góc A H A ' ^
Xét tam giác AIA’ vuông tại I:
tan 60 0 = AA ' A H ⇒ AA ' = A H . tan 60 0 = a 3 2 . 3 = 3 a 2
Thể tích lăng trụ
V = AA ' . S A ' B ' C ' = 3 a 2 . a 2 3 4 = 3 a 3 3 8 (dvtt)

Chọn đáp án D.
Ta có A'A = A'B = A'C nên hình chiếu của A' là tâm đường tròn ngoại tiếp tam giác ABC.
Do tam giác ABC đều nên trọng tâm G là tâm đường tròn ngoại tiếp tam giác ABC.
![]()
AG là hình chiếu của A'A lên mặt phẳng (ABC)
Góc giữa A'A với mặt phẳng (ABC) là: A ' A G ^
Gọi H là trung điểm BC.
Ta có: 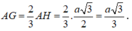
Xét tam giác A'AG vuông tại G:
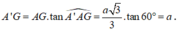
Diện tích tam giác đều ABC là:
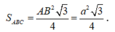
Thể tích khối lăng trụ ABC.A'B'C' là:
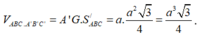
Chọn D.
Phương pháp: Sử dụng công thức tính thể tích lăng trụ.