Trong không gian Oxyz, cho hai điểm A 6 ; − 3 ; 4 , B a ; b ; c . Gọi M, N, P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ (Oxy), (Oxz), (Oyz). Biết rằng M, N, P nằm trên đoạn AB sao cho AM = MN = NP = PB. Tính giá trị của tổng a + b + c.
A. a+b+c = 11
B.a+b+c = -11
C.a+b+c = 17
D.a+b+c = -17


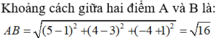
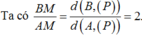
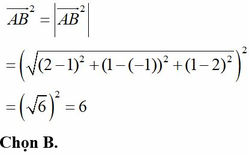
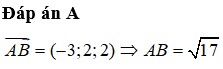
Đáp án B.
Các phương trình O x y : z = 0 ; O x y : x = 0 ; O x y : y = 0 . Giả sử M x M ; y M ; 0 , N x N ; 0 ; z N , P 0 ; y p ; z p . Tính theo giả thiết có M là trung điểm của AN nên ta có M 6 + x N 2 ; − 3 2 ; 4 + z N 2 . Do z M = 0 nên 4 + z N 2 = 0 ⇔ z N = − 4 ⇒ M x M ; − 3 2 ; 0 và N x N ; 0 ; − 4 .
Lại có N là trung điểm của MP nên N x M 2 ; 2 y P − 3 4 ; z P 2 .
Mà y N = 0 z N = − 4 nên 2 y P − 3 4 = 0 z P 2 = − 4 ⇔ y P = 3 2 z P = − 8 Khi đó P 0 ; 3 2 ; − 8 .
Từ
x M = 6 + x N 2 x M = x M 2 ⇔ 2 x M − x N = 6 x M − 2 x N = 0 ⇔ x M = 4 x N = 2
Vậy M 4 ; − 3 2 ; 0 , N 2 ; 0 ; − 4 .
Mặt khác
A B → = 2 A N → ⇔ x B − 6 = 2 ( 2 − 6 ) y B + 3 = 2 ( 0 + 3 ) z B − 4 = 2 ( − 4 − 4 ) ⇒ B ( − 2 ; 3 ; − 12 ) ⇒ a = − 2 b = 3 c = − 12 .
Vậy a + b + c = − 2 + 3 − 12 = − 11