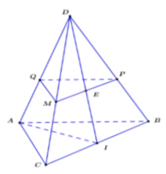
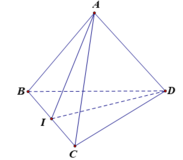
Cho tứ diện ABCD có ABC và DBC là hai tam giác đều cạnh chung BC = 2. Gọi I là trung điểm của BC, A I D ^ = 2 α mà cos 2 α = - 1 3 . Hãy xác định tâm O của mặt cầu ngoại tiếp tứ diện đó.
A. O là trung điểm của AD.
B. O là trung điểm của BD.
C. O thuộc mặt phẳng (ADB).
D. O là trung điểm của AB.

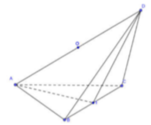
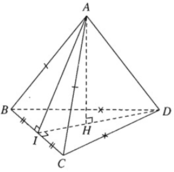
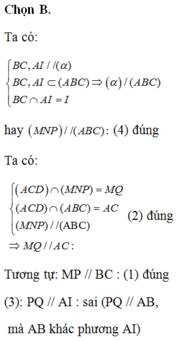
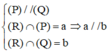
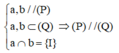


Chọn A.
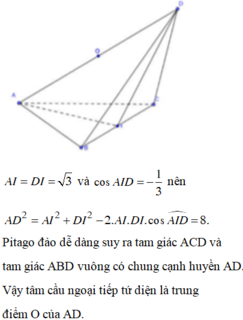
Pitago đảo dễ dàng suy ra tam giác ACD và tam giác ABD vuông có chung cạnh huyền AD.
Vậy tâm cầu ngoại tiếp tứ diện là trung điểm O của AD.