Một khối đá có hình là một khối cầu có bán kính R, người thợ thợ thủ công mỹ nghệ cần cắt và gọt viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của viên đá cảnh sau khi đã hoàn thiện.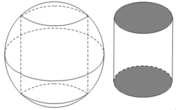
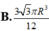
![]()
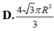
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi h và r (0 < h,r < 2R) lần lượt là chiều cao và bán kính mặt đáy của viên đá cảnh hình trụ ⇒ r 2 = R 2 - h 2 4 và áp dụng bất đẳng thức với 3 số x,y,z > 0 là:
x 2 + y 2 + z 2 ≥ 3 x 2 y 2 z 2 3 ⇔ x y z ≤ x 2 + y 2 + z 2 3 3 .
Thể tích viên đá là:
V = πr 2 h = π R 2 - h 2 4 h ⇒ V π 2 R 2 - h 2 4 R 2 - h 2 4 ≤ h 2 2 + R 2 - h 2 4 + R 2 - h 2 4 3 3 ⇒ V π 2 ≤ π 2 R 3 6 9 ⇒ V ≤ 4 πR 3 3 9

Đáp án B.
Trước hết ta có kết quả: Khối tứ diện ABCD có thể tích được tính theo công thức
![]()
Áp dụng kết quả này, ta có
![]()
= 6h
trong đó MN = PQ = 6 dm và h = d(MN;PQ) là chiều cao của hình trụ.
Từ giả thiết ta có h = 5 dm
Suy ra thể tích khối trụ là ![]() , với r = 3 dm
, với r = 3 dm
Do đó thể tích của lượng đá bị cắt bỏ là
![]()
Vậy phương án đúng là B.
Phân tích phương án nhiễu.
Phương án A và C: Sai do HS giải đúng nhưng làm tròn số bị sai hoặc lấy
Phương án D: Sai do HS chọn π = 3,141