Cho tam giác ABC có ˆB=ˆCB^=C^. Tia phân giác của góc A cắt BC tại D. Chứng minh:
a) Δ∆ADB = ADC
b) AB = AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2023
a: Xét ΔADB và ΔADC có
AD chung
góc BAD=góc CAD
AB=AC
=>ΔABD=ΔACD
b: Xét ΔDHB và ΔDHC có
DH chung
HB=HC
DB=DC
=>ΔDHB=ΔDHC
=>góc BDH=góc CDH
=>DH là phân giác của góc BDC
c: ΔABC cân tại A
mà AH là phân giác
nên AH vuông góc CB
7 tháng 1 2023
a: Xét ΔABD và ΔAMD có
AB=AM
góc BAD=góc MAD
AD chung
Do đó; ΔABD=ΔAMD
b: Xét ΔDBN và ΔDMC có
góc DBN=góc DMC
DB=DM
góc BDN=góc MDC
Do đó; ΔDBN=ΔDMC
=>BN=MC
c: Xét ΔANC có AB/BN=AM/MC
nên BM//CN
24 tháng 4 2023
`@` `\text {dnammv}`
`a,`
Xét `\Delta ABC:`
\(\widehat {A}+ \widehat {B}+ \widehat {C}=180^0 (\text {định lý tổng 3 góc trong 1} \Delta)\)
`90^0+ 60^0 + \hat {B}=180^0`
`-> \hat {B}=180^0-90^0-60^0=30^0`
`->`\(\widehat {A}> \widehat {B} > \widehat {C} (90^0>60^0>30^0)\)
`@` Theo định lý giữa góc và cạnh đối diện trong tam giác:
`-> \text {BC > AC > AB}`
`b,`
Xét `\Delta ABD` và `\Delta MBD`:
`\text {BD chung}`
\(\widehat {ABD}= \widehat {MBD}\) `(\text {tia phân giác}` `\hat {ABC})`
`AB = BC (g``t)`
`=> \Delta ABD = \Delta MBD (c-g-c)`
`c,` Vì `\Delta ABD = \Delta MBD (b)`
`-> \text {DA = DM (2 cạnh tương ứng)}`
`->` \(\widehat {BAD}= \widehat {BMD}\)`=90^0 (\text {2 góc tương ứng})`
Xét `\Delta ADN` và `\Delta MDC`:
`\text {DA = DM (CMT)}`
\(\widehat {ADN} = \widehat {MDC}\) `(\text {đối đỉnh})`
\(\widehat {BAD}= \widehat {BMD}\)`=90^0 (CMT)`
`=> \Delta ADN = \Delta MDC (cgv-gn)`
`-> \text {AN = MC (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{BA = BM (gt)}\\\text{AN = MC (CMT)}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{BN = BA+AN}\\\text{BC = BM+MC}\end{matrix}\right.\)
`=> \text {BN = BC}`
Xét `\Delta BAM:`
`\text {BA = BM}`
`-> \Delta BAM` cân tại `B`
`->`\(\widehat {BAM}= \widehat {BMA}=\)\(\dfrac{180^0-\widehat{B}}{2}\) `(1)`
Xét `\Delta BNC`:
`\text {BN = BC (CMT)}`
`-> \Delta BNC` cân tại `B`
`->`\(\widehat {BNC} = \widehat {BCN}=\)\(\dfrac{180-\widehat{B}}{2}\) `(2)`
Từ `(1)` và `(2)`
`->`\(\widehat {BNC}= \widehat {BAM}\)
Mà `2` góc này nằm ở bị trí đồng vị
`-> \text {AM // NC (tính chất 2 đường thẳng //)}`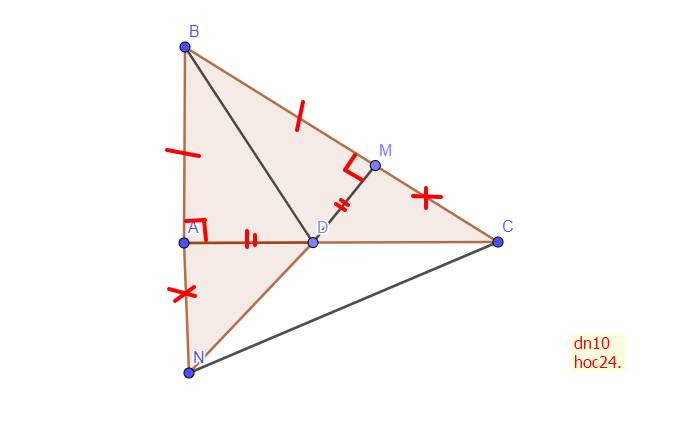
28 tháng 4 2023
a: AB<AC
=>góc B>góc C
góc ADB=góc DAC+góc ACD
góc ADC=góc BAD+góc ABD
mà góc ACD<góc ABD; góc BAD=góc CAD
nên góc ADB<góc ADC
b: Xét ΔABE có
AD vừa là đường cao, vừa là phân giác
=>ΔABE cân tại A
c: AD là phân giác
=>BD/AB=CD/AC
mà AB<AC
nên BD<CD
