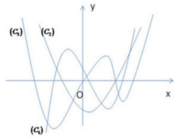
Cho hàm số y=f(x) liên tục và có đạo hàm cấp hai trên R. Đồ thị của các hàm số y=f(x), y=f'(x), y=f''(x) lần lượt là các đường cong nào trong hình vẽ bên.
A. C 3 , C 1 , C 2
B. C 1 , C 2 , C 3
C. C 3 , C 2 , C 1
D. C 1 , C 3 , C 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Dựa vào hình vẽ, ta thấy rằng:
Đồ thị C 3 có dạng đồ thị hàm số trùng phương.
Đồ thị C 2 có dạng đồ thị hàm số bậc hai (parabol)
Đồ thị C 1 có dạng đồ thị hàm số bậc ba
Vậy đồ thị của các hàm số
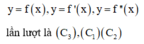

Chọn A
Gọi hàm số của các đồ thị ![]() tương ứng là
tương ứng là ![]() .
.
Ta thấy đồ thị ![]() có các điểm cực trị có hoành độ là nghiệm của phương trình
có các điểm cực trị có hoành độ là nghiệm của phương trình ![]() nên hàm số
nên hàm số ![]() là đạo hàm của hàm số
là đạo hàm của hàm số ![]() .
.
Đồ thị ![]() có các điểm cực trị có hoành độ là nghiệm của phương trình
có các điểm cực trị có hoành độ là nghiệm của phương trình ![]() nên hàm số
nên hàm số ![]() là đạo hàm của hàm số
là đạo hàm của hàm số ![]() .
.
Vậy, đồ thị các hàm số ![]() ,
, ![]() và
và ![]() theo thứ tự, lần lượt tương ứng với đường cong
theo thứ tự, lần lượt tương ứng với đường cong ![]() .
.

Đáp án là C
Các đồ thị hình vẽ bên chính là đồ thị của các hàm số lượng giác.

Đáp án C.
Ta có ![]() ∀
x
∈
R
∀
x
∈
R
Khi đó ![]()
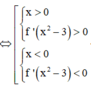
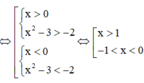
Suy ra hàm số đồng biến trên khoảng (–1;0) và (1;+ ∞)