Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB=AC=a và cạnh BAC=120 ° , cạnh bên BB'=a, gọi I là trung điểm của CC'. Côsin góc tạo bởi mặt phẳng (ABC) và (AB'I) bằng.
A. 20 10
B. 30
C. 30 10
D. 30 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:
Cách giải: Gọi J là giao điểm của B’I và BC. Suy ra AJ là giao tuyến của (AB’I) và (ABC).
Gọi K là hình chiếu của C lên AJ. Suy ra AJ vuông góc với KI.

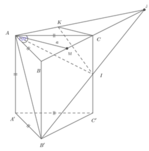
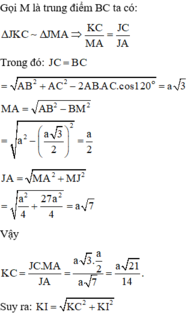
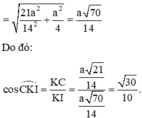

Đáp án C
Phương pháp: Phương pháp tọa độ hóa.
Cách giải:
Cách 1:
Gọi O là trung điểm của BC.
Tam giác ABC là tam giác cân, AB = AC = a, B A C ^ = 120 0
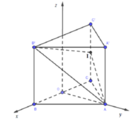
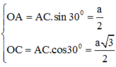
Ta gắn hệ trục tọa độ như hình bên:
Trong đó, O(0;0;0); A(0; a 2 ;0); B' ( a 3 2 ;0;a); I( - a 3 2 ;0; a 2 )
Mặt phẳng (ABC) trùng với mặt phẳng (Oxy) và có VTPT là n 1 → = ( 0 ; 0 ; 1 )
I B ' → = a 3 ; 0 ; a 2 ; I A → = a 3 2 ; a 2 ; - a 2
Mặt phẳng (IB’A) có 1 VTPT n 2 → = 2 3 ; 0 ; 1 ; 3 ; 1 ; - 1 = 1 ; 3 3 ; 2 3
Côsin góc giữa hai mặt phẳng (ABC) và (IB’A) :
cos((ABC);(AB'I)) = |cos(
n
1
→
;
n
2
→
)| = 
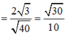
Cách 2:
Trong (ACC’A’) kéo dài AI cắt AC’tại D.
Trong (A’B’C’) kẻ A’H ⊥ B’D ta có:
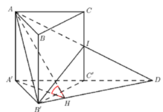
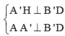
![]()
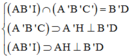
=> ![]()
Ta dễ dàng chứng minh được C’ là trung điểm của AD’
![]()
![]()
=> 
Xét tam giác A’B’D có
B'D = ![]()
![]()
=> 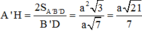
Xét tam giác vuông AA'H có :
![]()
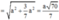
=> 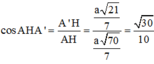

Gọi ![]()
Khi đó ![]()
Ta tính được ![]()
![]()
Ta có
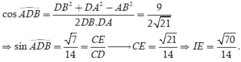
Vậy 
Chọn A.
Cách 2. Vì
∆
ABC là hình chiếu của
∆
AB'I trên mp (ABC) nên 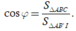

Đáp án B
Gọi a là độ dài cạnh hình lập phương. Thể tích khối lập phương: V 1 = a 3
Thể tích khối tứ diện: A B D A ' : V 2 = 1 3 . A A ' . S A B D = 1 3 . a . a 2 2 = a 3 6
Vậy V 1 = 6 V 2