Cho hàm số f(x) = x - 1 2 a x 2 + 4 a x - a + b - 2 , với a,b ∈ ℝ . Biết trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1. Hỏi trên đoạn - 2 ; - 5 4 , hàm số đạt giá trị nhỏ nhất tại giá trị nào của x?
A. x = - 5 4
B. x = - 4 3
C. x = - 3 2
D. x = -2

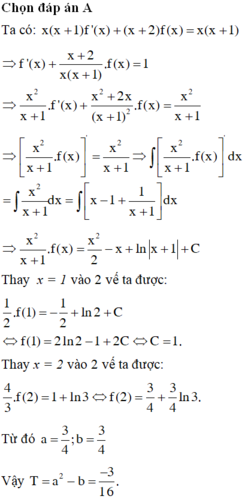
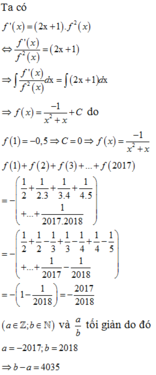

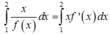
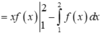
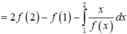



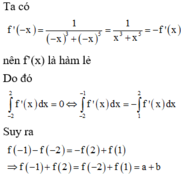

Chọn C
Tập xác định của hàm số là ℝ .
Ta có: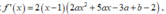
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
Khi đó f'(x) = 0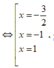 ( đều là các nghiệm đơn)
( đều là các nghiệm đơn)
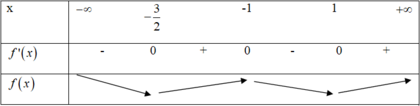
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4