Một khối hộp chữ nhật ABCD. A 1 B 1 C 1 D 1 có đáy ABCD là một hình vuông. Biết diện tích toàn phần của hình hộp đó là 32, thể tích lớn nhất mà khối hộp ABCD. A 1 B 1 C 1 D 1 là bao nhiêu?
A. 56 3 9
B. 70 3 9
C. 64 3 9
D. 80 3 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C

Ta có diện tích toàn phần của hình hộp chữ nhật là S = 32 = 2 a 2 + 4 a b = 2 ( a 2 + a b + a b ) ≥ 2 . 3 a 2 . a b . a b 3 = 6 ( a 2 b ) 2 3 = 6 V 2 3
⇒ V 2 3 ≤ 32 6 ⇔ V ≤ ( 16 3 ) 3 = 64 3 9

Chọn đáp án A
Thể tích của khối hộp chữ nhật có chiều cao bằng h, đáy là hình vuông cạnh a được tính theo công thức:
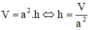 .
.
Diện tích toàn phần của hình hộp là:
![]()
![]()

Diện tích đáy là 81 cm2 suy ra chiều rộng là 9 cm
Diện tích toàn phần là 81 : 1/5 = 405 (cm2)
Diện tích xung quanh là 405 - 81 x 2 = 243 (cm2)
Chiều cao là 243 : 9 = 27 (cm)
Nếu sai thì mình xin lỗi
Bài 4: Diện tích toàn phần: 81 x 5 = 405(m2)
Diện tích xung quanh: 405 - (81x2) = 243 (m2)
Chiều cao: 324 : (9 x 4) = 6,75 (m) (cạnh của đáy bằng 9 vì 81 = 9 x 9)

ta có diện tích toàn phần của hình hộp là : \(81\times5=405cm^2\)
Vậy diện tích xung quanh của hình hộp là : \(405-81\times2=243cm^2\)
Mà hình vuông cạnh đáy có chiều dài là 9cm ( do 9x9 = 81)
thế nên chiều cao của hình hộp là : \(\frac{243}{4\times9}=6,75cm\)
tại sao phải lấy diện tích xung quanh chia cho một mặt đáy
Đáp án đúng : C