Một người nâng tấm ván AB có trọng lượng lượng 50 kg với lực F để ván nằm yên và hợp với mặt đường một góc 30o. Xác định độ lớn của lực F → khi lực F hướng vuông góc với tấm ván.
A. 125 3 N
B. 125 2 N
C. 250 2 N
D. 250 3 N
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: P = m g = 40.10 = 400 ( N )
a. Theo điều kiện cân bằng của Momen lực
M F → = M P → ⇒ F . d F = P . d P V ớ i d P = cos 30 0 . A B 2 ; d F = A B ⇒ F . A B = 400. cos 30 0 A B 2 ⇒ F = 100 3 ( N )

b. Theo điều kiện cân bằng của Momen lực
M F → = M P → ⇒ F . d F = P . d P V ớ i d P = cos 30 0 . A B 2 d F = cos 30 0 . A B ⇒ F . A B . cos 30 0 = 400. cos 30 0 . A B 2 ⇒ F = 200 ( N )


Áp dụng điều kiện cân bằng của thanh đối với trục quay tại điểm tiếp xúc với sàn ta có M F = M P
Fl = P(l/2).cos 30 ° ⇒ F = P 3 /4 = 200 3 /4 = 86,6(N)

Áp dụng điều kiện cân bằng của thanh đối với trục quay tại điểm tiếp xúc với sàn ta có M F = M P
Fl.cos 30 ° = P(l/2).cos 30 ° ⇒ F = P/2 = 100(N)

a)
để khúc gỗ không tượt
\(P< 2F_{ms}\) (hai tấm ván)
\(\Leftrightarrow\dfrac{P}{2\mu}< N\)
\(\Rightarrow N>50N\)
b) P-2Fms=m.a
\(\Rightarrow a=\)2m/s2
thời gian vật đi được h=1m
s=a.t2.0,5=1\(\Rightarrow t=\)1s
c) để vật trượt đều khi kéo lên với lực F
F-2Fms-P=0
\(\Rightarrow F=\)48N

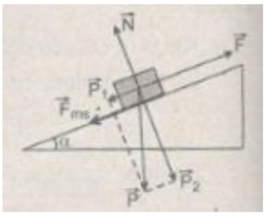
Chọn chiều chuyển động của vật m là chiều dương. Phương trình của định luật II Niu-tơn đối với vật m chuyển động trên mặt phẳng nghiêng như hình vẽ có dạng:
ma = F – P 1 - F m s
Với P 1 = mg.sin 30 ° ≈ 400 N.
F m s = μN = µmgcos 30 ° ≈ 13,8 N.
Khi vật chuyển động thẳng đều: a = 0, lực kéo có độ lớn:
F = P 1 + F m s ≈ 413,8 N
Do đó, công của lực kéo: A = Fs = 413,8.2,5 = 1034,5 J.
Đáp án A
Ta có: P = m g = 50.10 = 500 ( N )
Theo điều kiện cân bằng của momen lực
M F → = M P → ⇒ F . d F = P . d P
Với d P = cos 30 0 . A B 2 ; d f = A B
⇒ F . A B = 500. cos 30 0 A B 2 ⇒ F = 125 3 ( N )