Tìm hệ số của x 4 trong khai triển nhị thức Newton 2 x + 1 x 5 n với x > 0 biết n là số tự nhiên lớn nhất thỏa mãn A n 5 ≤ 18 A n - 2 4
A. 8064
B. 3360
C. 13440
D. 15360
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

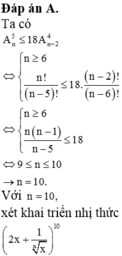
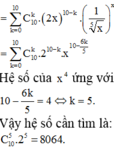

Đáp án A.
Ta có A n 5 ≤ 18 A n - 2 4 ⇔ n ≥ 6 n ! n - 5 ! ≤ 18 . n - 2 ! n - 6 ! ⇔ n ≥ 6 n n - 1 n - 5 ≤ 18 ⇔ 9 ≤ n ≤ 10 → n = 10 .
Với n = 10, xứt khai triển nhị thức
2 x + 1 x x 10 = ∑ k = 10 10 C 10 k . 2 x 10 - k . 1 x 5 x = ∑ k = 0 10 C 10 k . 2 10 - k . x 10 - 6 k 5 .
Hệ số của x 4 ứng với 10 - 6 k 5 = 4 ⇔ k = 5 . Vậy hệ số cần tìm là C 10 5 . 2 5 = 8064 .

Đáp án C
Ta có P ( x ) = 1 + 2 x 12 = ∑ k = 0 12 C 12 k 1 12 - k = ∑ k = 0 12 C 12 k 2 k x k .
Gọi a k = C 12 K 2 K , 0 ≤ k ≤ 12 , k ∈ ℕ là hệ số lớn nhất trong khai triển.
Suy ra a k ≥ a k + 1 a k ≥ a k - 1 ⇔ c 12 k 2 k ≥ c 12 k + 1 2 k + 1 c 12 k 2 k ≥ c 12 k - 1 2 k - 1
⇔ 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 11 - k ! k + 1 ! . 2 k + 1 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 13 - k ! k + 1 ! . 2 k - 1 ⇔ 1 12 - k ≥ 2 k + 1 1 k ≥ 1 2 13 - k
Vậy hệ số lớn nhất trong khai triển đã cho là a 8 = 2 8 c 12 8 = 126720 .