Cho hàm số y = x 3 + 3 x 2 - 1 . Biểu thức liên hệ giữa giá trị cực đại y C N ~ và giá trị cực tiểu y C T là
A. y C N ~ = 3 y C T
B. y C T = - 3 y C N ~
C. y C N ~ = - y C T
D. y C N ~ = - 3 y C T
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có y ' = 3 x 2 + 6 x = 3 x x + 2 ⇒ y ' = 0 ⇔ x = 0 x = − 2
Hàm số đạt cực đại tại x = − 2 ⇒ y C D = 3
Hàm số đạt cực tiểu tại x = 0 ⇒ y C T = − 1

Đáp án A
Xét hàm số y = x 3 - 2 x , ta có y ' = 3 x 2 - 2 ; y ' ' = 6 x
Phương trình
y ' = 0 ⇔ x 2 = 2 3 ⇔ x = ± 6 3 ⇒ y C T = - 4 6 9 y C D = 4 6 9 ⇒ y C T + y C D = 0

Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C

Phương pháp:
Quan sát bảng biến thiên và tìm điểm cực đại, cực tiểu và các giá trị cực đại, cực tiểu tương ứng.
Cách giải:
Số cách chọn là: 6.4 = 24 (cách). Quan sát bảng biến thiên ta thấy:
Hàm số đạt cực đại tại x = 2 và yCD = 3 .
Hàm số đạt cực tiểu tại x = 2 và yCT = 0 .
Vậy yCD = 3 và yCT = 0 .
Chọn: B

Đáp án B
TXĐ: D = R
Đạo hàm ![]()
Điều kiện để hàm số có cực đại và cực tiểu là ab < 0
Hàm số đạt cực đại tại A(0;3) ⇔ c = 3
Hàm số đạt cực tiểu tại 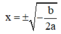 và điểm cực tiểu là B(1;-3), suy ra
và điểm cực tiểu là B(1;-3), suy ra
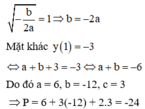

Đáp án A
y ' = x 2 + 4 x + 3 x + 2 2 ⇒ y ' = 0 ⇔ x 2 + 4 x + 3 = 0 ⇔ x = − 1 ⇒ y c t = 1 = n x = − 3 ⇒ y c d = − 3 = M ⇒ M 2 − 2 n = 7
Chọn đáp án D