Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng
A
M
N
luôn vuông góc với mặt phẳng
B
C
D
.
Gọi
V
1
;
V
2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính
V
1
+
V
2
?
A.
17
2
...
Đọc tiếp
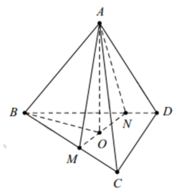
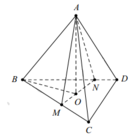
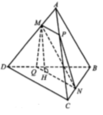
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng A M N luôn vuông góc với mặt phẳng B C D . Gọi V 1 ; V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2 ?
A. 17 2 216
B. 17 2 72
C. 17 2 144
D. 2 12
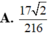
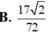
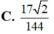
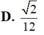
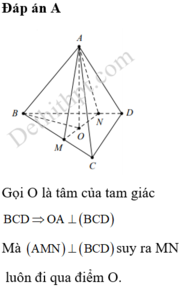
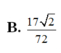
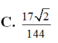
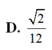
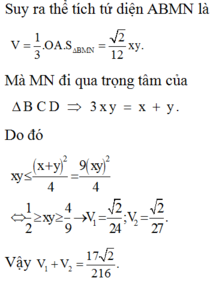
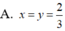
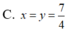
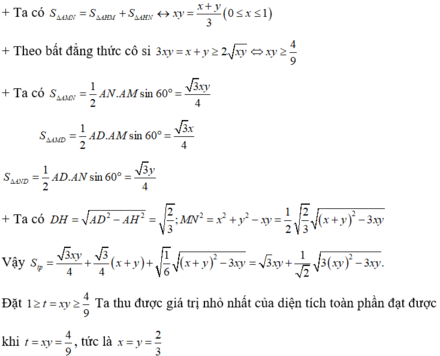
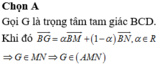
Đáp án A
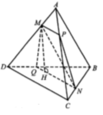
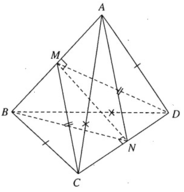
Gọi O là tâm của tam giác B C D ⇒ O A ⊥ B C D
Mà A M N ⊥ B C D suy ra MN luôn đi qua điểm O.
Đặt B M = x , B N = y ⇒ S Δ B M N = 1 2 . B M . B N . sin M B N ^ = 3 4 x y .
Tam giác ABO vuông tại O
Suy ra thể tích tứ diện ABMN là V = 1 3 . O A . S Δ B M N = 2 12 x y .
Mà MN đi qua trọng tâm của Δ B C D ⇒ 3 x y = x + y .
Do đó:
x y ≤ x + y 2 4 = 9 x y 2 4 ⇔ 1 2 ≥ x y ≥ 4 9 → V 1 = 2 24 ; V 2 = 2 27 .
Vậy V 1 + V 2 = 17 2 216 .