Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
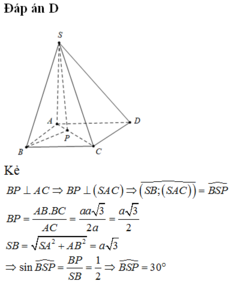
Đáp án A
Gọi I là giao điểm của AC và BD.
Ta có S A ⊥ A B C D ⇒ S A ⊥ B D . Lại có A C ⊥ B D (tính chất hình vuông).
Suy ra B D ⊥ S A C . Do đó hình chiếu của SB trên (SAC) là SI. Suy ra góc giữa đường thẳng SB và mặt phẳng (SAC) là góc giữa SB và SI, tức là góc ISB (do tam giác ISB vuông tại I nên I S B ^ là góc nhọn). Ta có:
S B = S A 2 + A B 2 = a 2 + a 2 = a 2 , I B = B D 2 = A 2 2
D o đ ó sin I S B = I B S B = 1 2 ⇒ I S B = 30 °
Đáp án A.
Cách 1: Gọi I là giao điểm của AC và BD.
Ta có S A ⊥ A B C D ⇒ S A ⊥ B D . Lại có A C ⊥ B D (tính chất hình vuông).
Suy ra B D ⊥ S A C . Do đó hình chiếu của SB trên S A C là SI. Suy ra góc giữa đường thẳng SB và mặt phẳng S A C là góc giữa SB và SI, tức là góc I S B ^ (do tam giác ISB vuông tại I nên I S B ^ là góc nhọn). Ta có:
S B = S A 2 + A B 2 = a 2 + a 2 = a 2 , I B = B D 2 = a 2 2
Do đó
sin I S B ^ = I B S B = 1 2 ⇒ I S B ^ = 30 °
Cách 2: (Phương pháp tọa độ hóa) Không mất tổng quát, gán tọa độ như sau:
A 0 ; 0 ; 0 , B 1 ; 0 ; 0 , D 0 ; 1 ; 0 , S 0 ; 0 ; 1 Khi đó C 1 ; 1 ; 0 .
Ta có S A → = 0 ; 0 ; − 1 , S C → = 1 ; 1 ; − 1 , S B → = 1 ; 0 ; − 1
Đặt n → = S A → , S C → = 1 ; − 1 ; 0 . Khi đó n → là một VTPT của S A C .
Gọi α là góc giữa đường thẳng SB và mặt phẳng S A C , β là góc giữa vecto n → và vecto S B → . Ta có
sin α = cos β = n → . S B → n → . S B → = 1 2 . 2 = 1 2 ⇒ α = 30 °
Đáp án C
Phương pháp: Thể tích khối chóp V = 1 3 S d . h : h là chiều cao của khối chóp, S là diện tích đáy.
Phương pháp xác định góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng và mặt phẳng chính là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng.
