Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là trung điểm SB và G là trọng tâm của tam giác SBC. Gọi V, V' lần lượt là thể tích của các khối chóp M.ABC và G.ABD tính tỉ số V V '
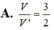
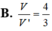
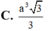
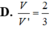
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A

Ta có
V ' = 1 3 d M ; A B C C . S A B C = 1 3 . 1 2 d S ; A B C D . 1 2 S A B C D V ' = 1 3 d G ; A B D . S A B D = 1 3 . 1 3 d S ; A B C D . 1 2 S A B C D
Do đó V V ' = 3 2

Đáp án A
Gọi H và K lần lượt là hình chiếu của M và G xuống ABCD
Ta có V V ' = 1 3 M H . S A B C 1 3 G K . S A D B = 3 2 . 1 2 S A B C D 1 2 S A B C D = 3 2

Đáp án C
Giả sử S D → = m . S M → ; S B → = n . S N → .
S A → + S C → = S B → + S D →
Do A; M; N; K đồng phẳng nên m + n = 3 .
V S . A K M V S . A B C = 1 2 .1. 1 m = 1 2 m ⇒ V S . A K M V = 1 4 m
Tương tự ta có V S . A K N V = 1 4 n ⇒ V ' V = 1 4 . m + n m n = 3 4 m n ≥ 3 m + n 2 = 3 3 2 = 1 3 .
Dấu bằng xảy ra khi m = n = 1,5 .