Trong phòng thí nghiệm, người ta còn dùng cân Rôbécvan để xác định chính xác thể tích của vật rắn không thấm nước. Cách làm như sau:- Dùng một loại bình đặc biệt có nút rỗng bằng thủy tinh có thể vặn khít vào cổ bình. Giữa nút có một ống thủy tinh nhỏ, trên có khắc một “ vạch đánh dấu” cho phép xác định một cách chính xác thể tích của nước trong bình tới vạch đánh dấu (...
Đọc tiếp
Trong phòng thí nghiệm, người ta còn dùng cân Rôbécvan để xác định chính xác thể tích của vật rắn không thấm nước. Cách làm như sau:
- Dùng một loại bình đặc biệt có nút rỗng bằng thủy tinh có thể vặn khít vào cổ bình. Giữa nút có một ống thủy tinh nhỏ, trên có khắc một “ vạch đánh dấu” cho phép xác định một cách chính xác thể tích của nước trong bình tới vạch đánh dấu ( hình 5.4a)
- Dùng cân Rôbécvan cân 2 lần:
+ Lần thứ nhất : đặt lên đĩa cân bình chứa nước cất tới vạch đánh dấu, vật cần xác định thể tích, các quả cân có khối lượng tổng cộng làm m1, sao cho cân bằng với một vật nặng T đặt trên đĩa cân còn lại ( vật T được gọi là tải) (H.5.4b)
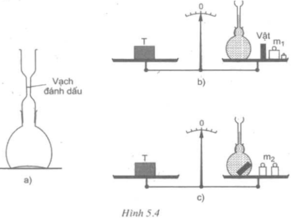
+ Lần thứ hai: Lấy bình ra khỏi đĩa cân, mở nút, đổ bớt nước cất trong bình, thả vật cần xác định thể tích vào bình, đậy nút và cho thêm nước vào bình tới vạch đánh dấu, rồi đặt lại bình lên đĩa cân. Thay các quả cân khối lượng m1, bằng các quả cân khối lượng m2 để cân lại cân bằng ( H.5.4c). Biết 1 gam nước cất có thể bằng 1cm3. Hãy chứng minh rằng thể tích V của vật tính ra cm3 có độ lớn đúng bằng độ lớn của hiệu các khối lượng (m2 – m1) tính ra gam
Tại sao cách xác định thể tích này lại chính xác hơn cách đo thể tích vật rắn bằng bình chia độ?
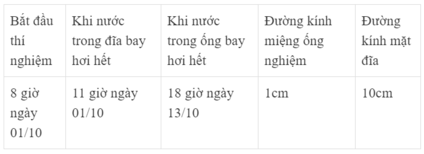

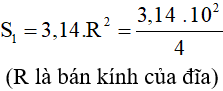
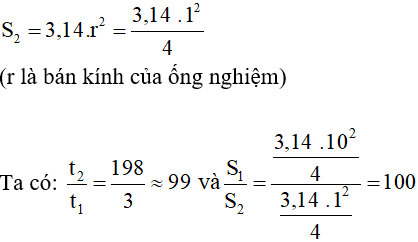
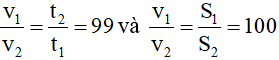

Thời gian nước trong đĩa bay hơi: t1 = 11 giờ - 8 giờ = 3 giờ
Thời gian nước trong ống nghiệm bay hơi hết:
t2 = (13 - 1) x 24 giờ + (18 giờ - 8 giờ) = 198 giờ
Diện tích mặt thoáng của nước trong đĩa:
Diện tích mặt thoáng của nước trong ống nghiệm:
Với cùng một lượng nước cho bay hơi, thời gian bay hơi càng nhỏ chứng tỏ tốc độ bay hơi càng lớn. Do đó nếu gọi v1 là tốc độ bay hơi của nước ở đĩa và v2 là tốc độ bay hơi của nước trong ống nghiệm.
Ta có:
Vậy một cách gần đúng, ta thấy tốc độ bay hơi tỉ lệ với diện tích mặt thoáng.